Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 25

Considere o campo de escoamento V → =   a x t   i ^   +   b   j ^ , em que a   =   0,1   s - 2   e b   =   4   m / s . As coordenadas são medidas em metros. Para a partícula que passa pelo ponto ( x ,   y )   =   ( 3 ,   1 ) no instante t   =   0 , trace a trajetória durante o intervalo de tempo de t   =   0   a t   =   3   s . Compare essa trajetória com as linhas de corrente que passam pelo mesmo ponto nos instantes t   =   1 ,   2   e 3   s .

Passo 1

Esse é mais um dos problemas de campo de velocidade, onde devemos encontrar o caminho para a partícula começando em ( 3,1 ) e outra trajetória através do mesmo ponto em t   =   1 ,   2   e   3   s . Assim, utilizaremos as equações para as linhas de corrente:

u p = d x d t         e       v p = d y d t

v u = d y d x

Passo 2

Para os caminhos, fazemos

u p = d x d t = A x t                 v p = d y d t = b

Agora, separamos as variáveis e integramos

d x x = A t   d t                   d y = b   d t                  

ln ⁡ x = 1 2 A   t 2 + C 1                                   y = b t + C 2

Usando a condição inicial ( x ,   y ) = ( 3,1 ) e os valores fornecidos para a e b , a solução é:

x = 3 e 0,05 t 2               e         y = 4 t + 1

Passo 3

Assim, para linhas de fluxo (a qualquer momento t):

v u = d y d x = b A x t

Agora, separamos as variáveis e integramos

d y = b A t d x x

y = b A t ln ⁡ x + C

Então, aplicando os valores de a e b , juntamente com o ponto ( 3,1 ) :

1 = 4 0,1   t ln ⁡ 3 + C         ∴           C = 1 - 4 0,1   t ln ⁡ 3

y = 4 0,1   t ln ⁡ 3 + 1 - 4 0,1   t ln ⁡ 3

y = 1 + 40 t ln ⁡ x 3

O gráfico para o intervalo de t   = 0   a t = 3   s , utilizando a equação acima é:

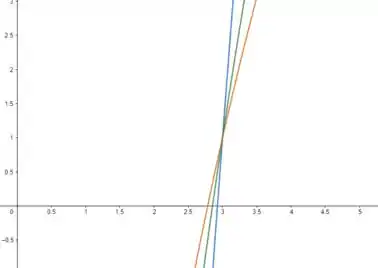
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Umescoamentoédescritopelocampodevelocidade V → = A x + B i + - A y j , em que A = 3 m m m e b = 6 m s . Trace algumas linhas de corrente no plano x y , incluindo aquela que passa pelo ponto x , y = 0,
Paraoscamposdevelocidadedadosabaixo,determine: a.Seocampodeescoamentoéuni,bioutridimensional,eporquê. b.Seoescoamentoéemregimepermanenteoutransiente,eporquê.(Asquantidadesaebsãoconstantes.) 1 → V = a
Umlíquidoviscosoécisalhadoentredoisdiscosparalelos;odiscosuperiorgiraeoinferioréfixo.Ocampodevelocidadeentreos discosédadopor → V=ê θ ω z / h ê .(Aorigemdascoordenadasestálocalizadanocentrododiscoinfe
Umcampodevelocidadeédadopor V → = a x 3 i + b x y 3 j , em que a = 1 m - 2 s - 1 ,b = 1 m - 3 s - 1 . Determine a equação das linhas de corrente para qualquer tempo t . Trace diversas linhas de corren
Paraoscamposdevelocidadedadosabaixo,determine: a.Seocampodeescoamentoéuni,bioutridimensional,eporquê. b.Seoescoamentoéemregimepermanenteoutransiente,eporquê.(Asquantidadesaeb sãoconstantes.) 1 v → = a