Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 7
O campo de velocidade é dado por , em que Determine a equação das linhas de corrente para qualquer tempo . Trace diversas linhas de corrente no primeiro quadrante para e
Passo 1
Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Este problema nos pede para obter uma equação para as linhas de corrente do escoamento e para traçarmos diversas linhas de corrente para valores no primeiro quadrante. Portanto:
Agora, vamos separar as variáveis:
Integrando:
Passo 2
Com isso, nossos gráficos ficam da seguinte forma. Para , temos:
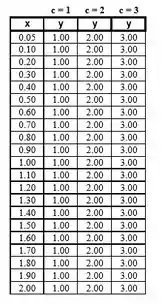
Para :
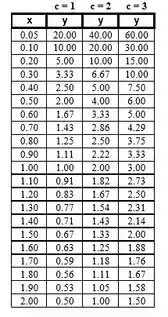
Por fim, para :
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Dois discos são dispostos coaxialmente face a face, separados por um filme de óleo lubrificante de espessura ε pequena. Aplicando-se um momento no disco 1 , ele inicia um movimento em torno de seu eix
No sistema da figura, o corpo cilíndrico de peso G desce com velocidade constante v = 2m / s , fazendo o eixo girar. Dados μ = 10 - 3N ⋅ s / m 2 ; L = 2 / πm ; D e = 50,2c m ; D i = 50c m ; d = 10c m
A placa da figura tem uma área de 4m 2 e espessura desprezível. Entre a placa e o solo existe um fluido que escoa, formando um diagrama de velocidades dado por v = 20 y v m á x 1 - 5 y á . A viscosida
Um fluido escoa sobre uma placa com o diagrama dado. Pede-se v = f y ;A tensão de cisalhamento junto à placa.
O turbocompressor de um motor de combustão interna tem uma rotação de 120.000r p m ω = 2 π n . Os mancais do eixo são flutuantes e giram com uma certa rotação. São dados: μ = 8 × 10 - 3N ⋅ s / m 2 ; D