Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo Exercícios Selecionados.- - Ex. 28
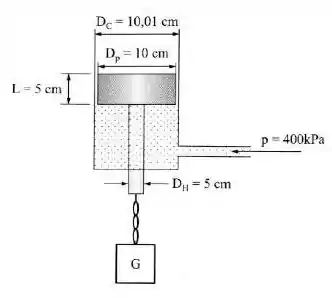
O pistão da figura levanta, com velocidade constante, um peso sob a ação de uma pressão. Entre o pistão e o cilindro existe uma película de lubrificante ; .
Qual a velocidade de subida do peso, supondo desprezíveis os pesos da haste e do pistão?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Fazendo o balanço de forças, temos que:
A força de cisalhamento é dada por:
Sabemos que:
A área de aplicação da pressão . Considerando a área de seção transversal do pistão menos a área do eixo do pistão de diâmetro :
A força tangencial é dada por:
Igualando as parcelas, temos que:
Substituindo as variáveis e resolvendo, temos que:
Resposta
Exercícios de Livros Relacionados
Na figura, uma placa de espessura desprezível e área A 1 = 2m 2 desloca-se com v = 5m / s constante, na interface de dois fluidos, tracionada por uma força F = 400N . Na parte superior, ε = 1m m e o d
UmcampodevelocidadeéespecificadocomoemqueV → = a x y i ^+ b y 2 j ^ emquea=2m−1s−1,b=−6m−1s−1eascoordenadassão medidasemmetros.Ocampodeescoamentoéuni,bioutridimensional?Porquê?Calculeascomponentesdave
Para o campo de velocidade em que V → = A x 2 y i ^ + B x y 2 j ^ , em que A = 2m - 2 s - 1 e B = 1m - 2 s - 1 , e as coordenadas são medidas em metros, obtenha uma equação para as linhas de corrente
Ocampodevelocidadeemque V → A x i ^ - A y j ^ , em que A = 2 s - 1 , pode ser interpretado para representar o escoamento em um canto.Determineumaequaçãoparaaslinhasde corrente do escoamento. Trace div
Umescoamentoédescritopelocampodevelocidade V → = A x + B i + - A y j , em que A = 3 m m m e b = 6 m s . Trace algumas linhas de corrente no plano x y , incluindo aquela que passa pelo ponto x , y = 0,