Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 65
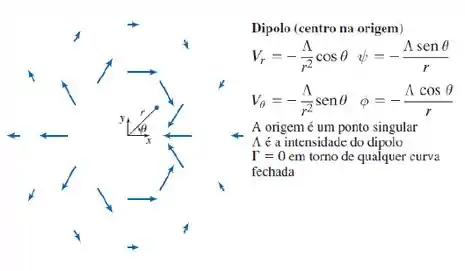
O campo de velocidade para um dipolo plano é dado na Tabela 6.2. Se , a massa específica do fluido é e a pressão no infinito é 100 kPa, trace um gráfico da pressão ao longo do eixo , de a , e de a .
Passo 1
Tá legal, o campo de velocidades dado está em coordenadas polares, e nós temos que analisar a pressão ao longo do eixo , nesse caso, sabemos que os pontos ao longo de possuem coordenadas e , dessa forma, as equaçãoes para a velocidade se tornam:
Dessa forma, o módulo da velocidade será:
Agora, para um ponto no infinito , as velocidades se tornam:
E, então, para esse ponto o módulo da velocidade é:
Passo 2
Agora vamos aplicar a equação de Bernoulli entre o ponto 1 com coordenadas e o ponto 2 que escolheremos como ficando no infinito, mas ainda sobre o eixo (pois sabemos que nesse ponto temos pressão atmosférica):
Como o enunciado não mencionou nada a respeito, podemos desconsiderar a diferença entre as cotas e . Então, substituindo os valores conhecidos, temos:
Passo 3
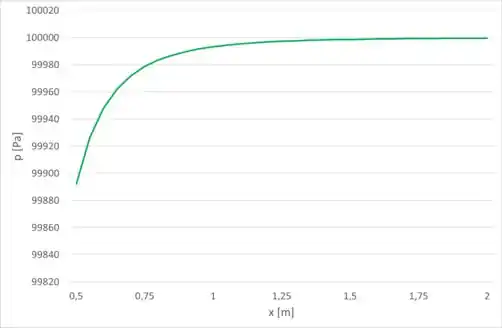
O gráfico que representa a pressão de até é:
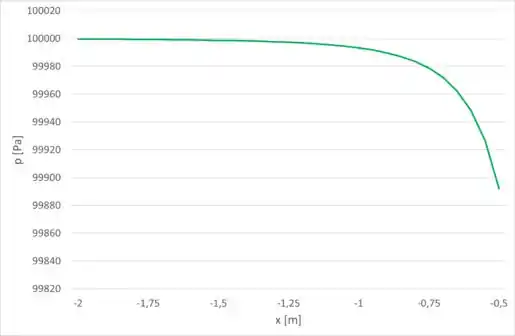
O gráfico que representa a pressão de até é:
