Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 64

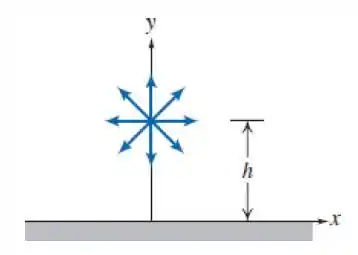
O campo de velocidade para uma fonte plana a uma distância h acima de uma parede infinita alinhada ao longo do eixo x foi dado no Problema 6.8. Usando os dados desse problema, trace um gráfico da distribuição de pressões ao longo da parede, de x = - 10 h a x = + 10 h (considere que a pressão no infinito é atmosférica). Determine a força resultante sobre a parede, se a pressão sobre a superfície inferior for atmosférica. A força tende a puxar a parede em direção à fonte ou a afastá-la da fonte?

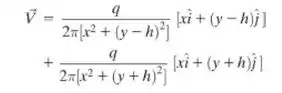
Passo 1

Tá legal, vamos começar o exercício separando as componentes de velocidade nas direções i → e j → :

u = q x 2 π x 2 + y - h 2 + q x 2 π x 2 + y + h 2

v = q ( y - h ) 2 π x 2 + y - h 2 + q y + h 2 π x 2 + y + h 2

Sabemos que o módulo da velocidade será dado por:

V 2 = u 2 + v 2 → V = u 2 + v 2

Passo 2

Agora vamos aplicar a equação de Bernoulli entre o ponto 1 com coordenadas ( x , 0 ) e o ponto 2 que escolheremos como ficando no infinito (pois sabemos que nesse ponto temos pressão atmosférica):

p 1 ρ + v 1 2 2 + g z 1 = p 2 ρ + v 2 2 2 + g z 2

Agora vamos observar novamente os termos de velocidade:

u = q x 2 π x 2 + y - h 2 + q x 2 π x 2 + y + h 2

v = q ( y - h ) 2 π x 2 + y - h 2 + q y + h 2 π x 2 + y + h 2

Podemos notar que o termo no numerador cresce com expoente 1 e os termos no denominador crescem com expoente 2, então, isso significa que conforme aumentamos as coordenadas x e y , o denominador cresce mais rápido do que o numerador, dessa forma, no infinito, essas velocidades tenderiam a zero, então, temos que v 2 = 0 .

Agora analisando o ponto ( x , 0 ) , substituindo essas coordenadas nas componentes de velocidade, temos:

u = q x 2 π x 2 + 0 - h 2 + q x 2 π x 2 + 0 + h 2 → u = q x π x 2 + h 2

v = q ( 0 - h ) 2 π x 2 + h 2 + q 0 + h 2 π x 2 + 0 + h 2 = - q h 2 π x 2 + h 2 + q h 2 π x 2 + h 2 → v = 0

E dessa forma, teríamos o módulo de v 1 como:

v 1 = q x π x 2 + h 2 2 + 0 2 → v 1 = q x π x 2 + h 2

Passo 3

Então, substituindo os valores conhecidos na equação de Bernoulli, temos:

p 1 ρ + v 1 2 2 + g z 1 = p 2 ρ + v 2 2 2 + g z 2

p 1 ρ + q x π x 2 + h 2 2 2 = p a t m ρ + 0 2 2

Então, fazendo p a t m = 0 para obter o valor da pressão p 1 já em forma manométrica, temos a seguinte equação:

p 1 = - ρ 2 q x π x 2 + h 2 2

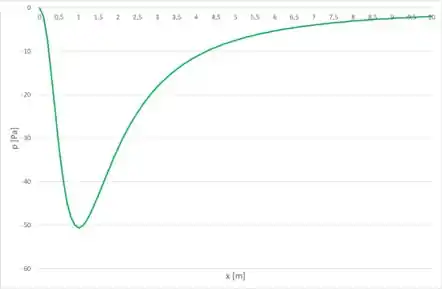
O gráfico que representa a distribuição de pressão é dado por:

Passo 4

A força resultante sobre a parede pode ser obtida integrando a pressão entre os limites inferior e superior, que nada mais é do que a pressão manométrica que encontramos no passo 3, então, temos:

F = ∫ - 10 h 10 h p s u p e r i o r - p i n f e r i o r d x = ∫ - 10 h 10 h p 1 d x

F = ∫ - 10 h 10 h - ρ 2 q x π x 2 + h 2 2 d x = - ρ q 2 2 π 2 ∫ - 10 h 10 h x 2 x 2 + h 2 2 d x

Agora, resolvendo essa integral com o auxílio de uma calculadora, temos:

F = - ρ q 2 2 π 2 1 2 1 h arctg ⁡ x h - x 2 ( x 2 + h 2 ) - 10 h 10 h

Subsituindo os limites de integração, temos:

F = - ρ q 2 2 π 2 1 2 1 h a r c t g 10 h h - 10 h 2 100 h 2 + h 2 - 1 2 1 h a r c t g - 10 h h - - 10 h 2 100 h 2 + h 2

F = - ρ q 2 2 π 2 1 2 1 h a r c t g 10 - 10 2 101 h - 1 2 1 h a r c t g - 10 - - 10 2 101 h

F = - ρ q 2 4 π 2 h a r c t g 10 - 10 2 101 - a r c t g - 10 - - 10 2 101

F = - ρ q 2 4 π 2 h a r c t g 10 - 10 2 101 - a r c t g - 10 - - 10 2 101

Substituindo os valores conhecidos e fazendo q = 2 e h = 1 (dados fornecidos no Problema 6.8), temos:

F = - 999 2 2 4 π 2 1 1,471 - 0,0495 - - 1,471 + 0,0495 → F = - 287,8   N

Resposta

F = - 287,8   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o tanque de armazenagem da Figura P 3.153 . Use a equação de Bernoulli para deduzir uma fórmula para a distância X em que o jato livre, saindo horizontalmente, irá atingir o piso, em função
Desprezar o atrito às vezes pode levar a resultados estranhos. Alguém lhe pediu para analisar e discutir o seguinte exemplo na Figura P A 3.5 . Um ventilador sopra ar através de um duto da seção 1 par
Na Figura P4.26 são definidas coordenadas curvilíneas, ou de linha de corrente, em que n é normal à linha de corrente no plano do raio de curvatura R. A equação da quantidade de movimento sem atrito d
Como mencionado na Seção 4.10, o perfil de velocidade para escoamento laminar entre duas placas, como na Figura P4.41, é u = 4 u m á x y h - y h 2v = w = 0 á Se a temperatura em ambas as paredes é T p
Reanalise o problema 3.54 para estimar a leitura no manômetro h através da equação de Bernoulli. Para h = 58 cm do problema 3.54, qual é a perda de carga?