Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 153

Considere o tanque de armazenagem da Figura P 3.153 . Use a equação de Bernoulli para deduzir uma fórmula para a distância X em que o jato livre, saindo horizontalmente, irá atingir o piso, em função de h e H . Para qual razão h / H a distância X será máxima? Esboce as três trajetórias para h / H = 0,4 , 0,5 e 0,6

Passo 1

E aí, tudo bem? Bora matar essa questão comigo!

Primeiro vamos expressar nossas variáveis de velocidade e tempo de queda:

V 0 = 2 g H - h

t q = 2 h g

Como bem conhecemos:

X = V 0 ⋅ t q

Logo:

X = 2 g H - h ⋅ 2 h g

X = 2 h H - h

Passo 2

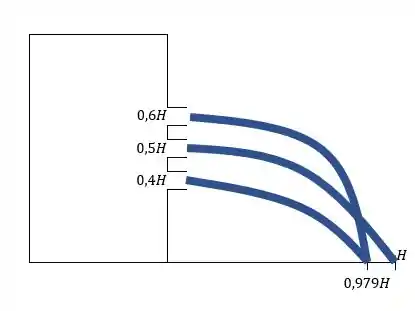
Agora vamos esboçar nosso problema.

Como:

X = 2 h H - h

X m á x ocorrerá em H / 2   vejamos:

X = 2 H 2 H - H 2 = 2 ⋅ H 2

X m á x = H

Calculando os valores desejados na questão:

X = 2 2 H 5 H - 2 H 5

X ≈ 0,979 H

X = 2 3 H 5 H - 3 H 5

X ≈ 0,979 H

Agora fazendo um esboço da nossa função:

Isso é tudo pessoal, conseguimos mais uma! \o/

Resposta

X = 2 h H - h

X m á x   e m   h = H 2

Esboço, vide passo a passo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ar escoa subsonicamente em um duto onde o atrito é negligenciado. Quando calor é adicionado em uma quantidade de 948 kJ/kg, a pressão cai de p 1 = 200k P a para p 2 = 106k P a . Usando a teoria unidim
Como as fórmulas para escoamento compressível em duto se compartam para quedas de pressão pequenas? Admita que o ar a 20°C entre em um tubo de 1 cm de diâmetro e 3 m de comprimento. Se f - = 0,028 com
Um observador ao nível do mar não ouve uma aeronave voando a 6000 m de altitude padrão até 15 segundos depois dela ter passado por ele. Estime a velocidade da aeronave.Bem, primeiramente como você est
Ar a 550 kPa e 100°C entra em um tubo liso de 1 m de comprimento e em seguida passa por um segundo tubo liso para um reservatório a 30 kPa, como na figura abaixo. Utilizando o diagrama de Moody para d
Ar a 300 K escoa através de um duto com 50 m de comprimento e f = 0,019 . Qual é o diâmetro mínimo o qual não causará um choque se a velocidade na entrada é (a) 50 m/s, (b) 150 m/s e (c) 420 m/s?