Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 148
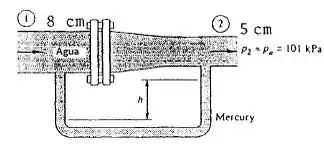
Reanalise o problema 3.54 para estimar a leitura no manômetro h através da equação de Bernoulli. Para h = 58 cm do problema 3.54, qual é a perda de carga?
Passo 1
E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)
No problema 3.54 temos que . Portanto pela conservação da massa teremos que .
Então pela equação de Bernoulli a gente acha a pressão de boa!
Passo 2
Aplicando a fórmula da hidrostática no manômetro, temos que:
Passo 3
Estimando o fator de atrito para h = 58 cm do problema 3.54, temos que:
Resposta
Exercícios de Livros Relacionados
Uma partícula movendo-se com velocidade uniforme no ar padrão ao nível do mar cria as duas esferas de perturbação mostradas na Figura P9.118. Calcule a velocidade da partícula e o número de Mach.
Uma sonda termistora, em forma de uma agulha paralela ao escoamento, indica uma temperatura estática de - 25 o C quando inserida em uma corrente de ar supersônica. Um cone de perturbação de semiângulo
A partícula na Figura P9.119 está se movendo supersonicamente no ar padrão ao nível do mar. Das duas esferas de perturbação dadas, calcule o número de Mach, a velocidade e o ângulo de Mach da partícul
Ar supersônico faz um giro de compressão de 5°, como na Figura P9.122. Calcule a pressão e o número de Mach a jusante e o ângulo da onda, e compare com a teoria de pequenas perturbações.
A partícula na Figura P9.120 está se movendo no ar padrão ao nível do mar. Das duas esferas de perturbação mostradas, calcule (a) a posição da partícula nesse instante e (b) a temperatura em ° C no po