Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 38
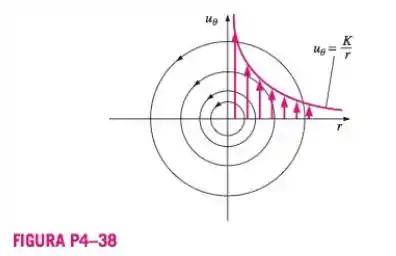
O campo da velocidade para uma linha de vórtices no plano (Figura ) é dado por
Onde é a intensidade da linha de vórtices. No caso com faça o gráfico de contorno do módulo da velocidade (velocidade escalar). Especificamente, desenhe curvas de velocidade constante e . Certifique-se de identificar velocidades escalares no seu gráfico.
Passo 1
Continuando com o fato de termos uma velocidade radial nula nós temos que a velocidade total do corpo será apenas a angular e que valerá:
Com , então:
Então para , nos dando curvas iguais a:
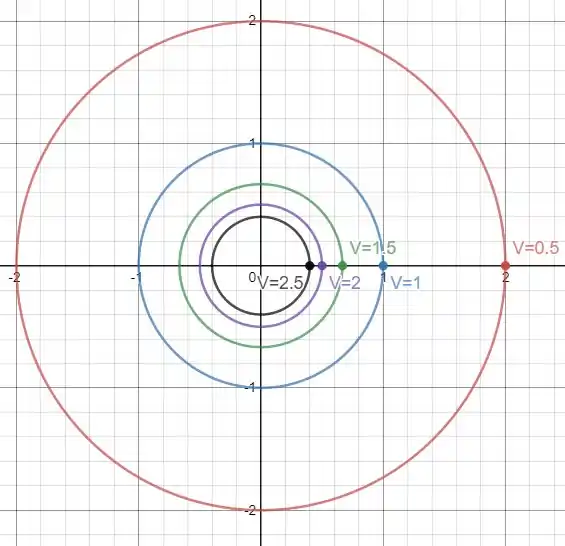
Se atente somente as cores.
Resposta
Gráfico do Passo 1
Exercícios de Livros Relacionados
Considere a forma geral do teorema de transporte de Reynolds (TTR) dada no Problema 4-75. Seja B s i s o momento angular H → =r →× mV → de um sistema de partículas de fluido, onde r → é o braço do mom
Reduza ao máximo a seguinte expressão: F t = d d t ∫ x = A t x = B t e - 2 x 2 d x Sugestão: Use o teorema de Leibnitz unidimensional.
Considere o escoamento de Poiseuille com simetria axial completamente desenvolvido – o escoamento em um tubo redondo de raio R (diâmetro D = 2 R ), com um gradiente de pressão forçado d P / d x movend
Considere o escoamento de Poiseuille com simetria axial do problema 4 - 87 , calcule as taxas de deformação linear nas deireções x e r e calcule a taxa de deformação por cisalhamento ϵ x r . O tensor
Combine seus resultados do problema 4-80 para formar o tensor da taxa de deformação bidimensional ε i j no plano x y ε i j = ε x xε x y ε y x ε y y Os eixos x e y são principais?