Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 88
Considere o escoamento de Poiseuille com simetria axial do problema , calcule as taxas de deformação linear nas deireções e e calcule a taxa de deformação por cisalhamento . O tensor taxa de deformação em coordenadas cilíndricas e , é
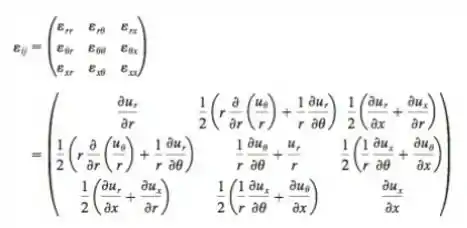
Passo 1
Fala aí galera, Bora pra mais uma questão de Mecânica dos Fluidos. Primeiramente, as taxas de deformação linear na direção e na direção são dadas por:
Portanto, não há taxa de deformação linear na direção ou . A taxa de deformação de cisalhamento no plano é:
As partículas de fluido nesse fluxo têm taxa de deformação de cisalhamento diferente de zero.
Resposta
Exercícios de Livros Relacionados
O escoamento de duto convergente é modelado pelo campo de velocidade permanente e bidimensional do Problema 4-15. O campo de pressão é dado por P = P 0 - ρ 2 ⋅ 2 ⋅ U 0 ⋅ b ⋅ x + b 2 ⋅ x 2 + y 2 onde P
Para o campo de velocidade do Problema 4-20, calcule a aceleração do fluido ao longo do eixo central do difusor como função de x e dos parâmetros dados. Para L = 2,0m , u e n t r a d a = 30,0m / s e u
Considere o escoamento permanente do ar através da parte do difusor de um túnel de vento (Figura P4-20). Ao longo do eixo central do difusor, a velocidade do ar diminui de u e n t r a d a para u s a í
Um campo de velocidade permanente, incompressível e bidimensional é dado pelas seguintes componentes do plano x y : u = 1,1 + 2,8 ⋅ x + 0,65 ⋅ y v = 0,98 - 2,1 ⋅ x - 2,8 ⋅ y Calcule o campo de acelera
Um campo de velocidade permanente, incompressível e bidimensional é dado pelas seguintes componentes do plano x y : u = 0,20 + 1,3 ⋅ x + 0,8 5 ⋅ y v = - 0,50 + 0,95 ⋅ x - 1,3 ⋅ y Calcule o campo de ac