Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 15
Para um canal retangular de largura , construa uma família de curvas de energia específica para . Quais são as energias específicas mínimas para essas curvas?
Passo 1
Beleza! Sabemos da equação 11.13 apresentada nessa seção que a energia específica é dada por:
Só que, nós podemos escrever a vazão em um canal retangular como sendo o produto da velocidade do escoamento nesse canal pela sua área transversal, que é dada pelo produto entre sua profundidade pela sua largura, então, temos:
Passo 2
Então, substituindo a expressão para na equação da energia específica, temos:
Então, construindo as curvas com as informações dadas no enunciado, temos:
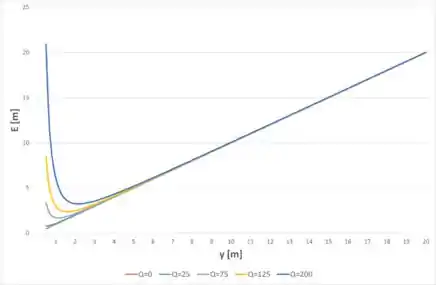
Passo 3
Agora, para encontrar as energias específicas mínimas exatas, podemos usar a fórmula para a profundidade crítica, apresenta na equação 11.23 dessa seção:
E, substituir o valor de encontrado em cada uma das equações das curvas, então, temos: