Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 93

A superfície exposta x = 0 de uma parede plana, com condutividade térmica k , é submetida à radiação de micro-ondas, que causa um aquecimento volumétrico que varia segundo

q ˙ x = q ˙ 0 1 - x L

em que e q ˙ e W / m 3   é uma constante. A fronteira em x = L está perfeitamente isolada, enquanto a superfície exposta é mantida a uma temperatura constante T o . Determine a distribuição de temperaturas T x em termos de x , L , k , q ˙ e e T e .

Passo 1

Fala Galera!!

Nessa questão queremos encontra a distribuição de temperaturas T x em termos de x , L , k , q ˙ 0 e T 0 . Podemos fazer o seguinte esquema que representa a parede plana descria no problema acima.

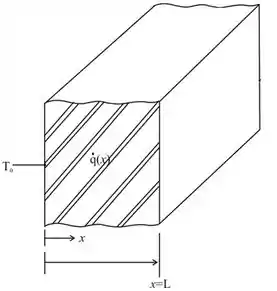
PRESSUPOSTOS:

(1) Condições em estado estacionário;

(2) Condução unidimensional na direção x ;

(3) Propriedades constantes;

(4) A condutividade térmica da parede plana é  k ;

Passo 2

Podemos resolver essa questão a partir da forma apropriada da equação de difusão de calor que é dada por:

d d x d T d x + q ˙ k = 0

Podemos substituir q ˙ por q ˙ x que foi fornecido no enunciado. Substituindo, temos:

d d x d T d x + q ˙ x k = 0

d d x d T d x + q ˙ 0 k 1 - x L = 0

d d x d T d x = - q ˙ 0 k 1 - x L

Separando as variáveis e integrando, temos:

d d T d x = - q ˙ 0 k 1 - x L d x

d T d x = - q ˙ 0 k x - x 2 2 L + C 1

Podemos separa as variáveis mais uma vez e integrar para encontrar a forma geral da distribuição de temperatura na parede plana. Assim temos:

d T = - q ˙ 0 k x - x 2 2 L + C 1 d x

T x = - q ˙ 0 k x 2 2 - x 3 6 L + C 1 x + C 2

Passo 3

Agora, vamos aplicar as condições de contorno para encontrar C 1 e C 2 . Temos que quando x = 0 temos que T 0 = T 0 e quando x = L temos que d T d x = 0 .

Aplicando a primeira condição x = 0 , temos:

T x = - q ˙ 0 k x 2 2 - x 3 6 L + C 1 x + C 2

T 0 = - q ˙ 0 k 0 2 2 - 0 3 6 L + C 1 0 + C 2

C 2 = T 0

Aplicando a segunda condição x = L , temos:

d T d x = - q ˙ 0 k x - x 2 2 L + C 1

0 = - q ˙ 0 k L - L 2 2 L + C 1

C 1 = q ˙ 0 k L - L 2

C 1 = q ˙ 0 L 2 k

Passo 4

Substituindo C 1 e C 2 na equação da distribuição de temperatura na parede plana, temos:

T x = - q ˙ 0 k x 2 2 - x 3 6 L + C 1 x + C 2

T x = - q ˙ 0 k x 2 2 - x 3 6 L + q ˙ 0 L 2 k x + T 0

T x = q ˙ 0 2 k L x - x 2 + x 3 3 L + T 0

Portanto, a distribuição de temperatura é:

T x = q ˙ 0 2 k L x - x 2 + x 3 3 L + T 0

Resposta

T x = q ˙ 0 2 k L x - x 2 + x 3 3 L + T 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um nanotubo de carbono está suspenso atravessando uma vala de largura s = 5 mm que separa duas ilhas, cada uma a T ∞ = 300K . Um feixe laser irradia o nanotubo, a uma distância ξ da ilha esquerda, for
Um bastão muito longo, com 5 mm de diâmetro e condutividade térmica uniforme k = 25 W m K , é submetido a um processo de tratamento térmico. Sua porção central, com 30 mm de comprimento, está envolta
Um bastão de metal de comprimento 2L, diâmetro D e condutividade térmica k está encravado em uma parede de um isolante perfeito, expondo a metade do seu comprimento a uma corrente de ar que se encontr
No Problema 1.71, considere os terminais que conectam o transistor à placa do circuito. Estes terminais possuem condutividade térmica k, espessura t, largura w e comprimento L. Uma extremidade do term
Considere uma superfície estendida de seção transversal retangular com transferência de calor na direção longitudinal. Nesse problema procuramos determinar condições nas quais a diferença de temperatu