Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 87
Considere a parede composta do Exemplo 3.7. Na seção de Comentários, distribuições de temperaturas na parede foram determinadas considerando resistência de contato desprezível entre os materiais e . Calcule e represente graficamente as distribuições de temperaturas para uma resistência térmica de contato igual a .
Passo 1
Fala Galera!!
Nessa questão queremos determinar a distribuição de temperatura na parede composta e representar graficamente.
PRESSUPOSTOS:
(1) condições de estado estacionário;
(2) condução unidimensional com propriedades constantes;
(3) a superfície interna do material A é adiabática.
DADOS FORNECIDOS:
Geração de calor uniforme na parede A:
Condutividade térmica da parede A:
Espessura da parede A:
Condutividade térmica da parede B:
Espessura da parede B:
Temperatura da corrente de água:
Coeficiente de transferência de calor por convecção:
Resistência térmica de contato:
Passo 2
Para resolver essa questão, podemos fazer o seguinte esquema para a parede composta de material A e B do exemplo 3.7:
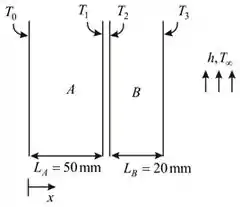
Também podemos fazer um esquema para o circuito equivalente térmico da resistência de contato para o lado direito do material B, como mostrado abaixo:
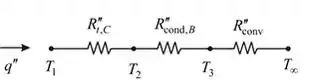
Aqui, é a resistência de contato térmico, é a resistência de condução no material B e é a resistência de convecção.
Passo 3
Temos que no material A, apresenta geração uniforme de calor, assim, a distribuição de temperatura pode ser dada pela equação 3.47. Assim temos:
Considerando o esquema feito no passo anterior, a distribuição de temperatura no material A fica da seguinte maneira:
Passo 4
Temos que no material B, não apresenta geração uniforme de calor, assim, a distribuição de temperatura é uniforme e pode ser dada pela equação 3.2. Assim temos:
Considerando o esquema feito no passo 2, podemos encontrar as constantes para determinar a distribuição de temperatura no material B. Assim temos:
Para
Para
Substituindo em , temos o seguinte:
Substituindo na equação de distribuição de temperatura, temos:
Na interface entre os dois materiais, , a distribuição de temperatura mostrará uma descontinuidade.
Passo 5
Agora, precisamos determinar , e para colocar nas equações de distribuição de temperatura encontradas nos passos anteriores. Considerando o circuito térmico acima, incluindo a resistência de contato térmico, temos o seguinte:
Podemos encontrar da seguinte maneira:
Substituindo os termos da equação acima pelos dados fornecidos, temos:
Passo 6
Podemos encontrar da seguinte maneira:
Substituindo os termos da equação acima pelos dados fornecidos, temos:
Passo 7
Podemos encontrar da seguinte maneira:
Substituindo os termos da equação acima pelos dados fornecidos, temos:
Passo 8
Podemos encontrar substituindo na equação encontrada no passo 3. Assim temos:
Passo 9
Portanto, temos que as distribuições de temperaturas na parede composta substituindo todos os valores encontrados são:
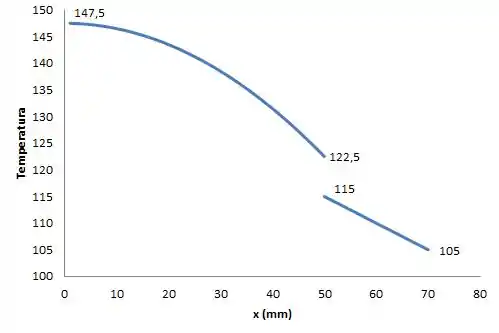
Passo 10
Podemos então traçar a distribuição de temperatura com todos os valores de temperatura conhecidos a partir das distribuições de temperaturas na parede composta encontradas acima. Assim temos:
