Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 11
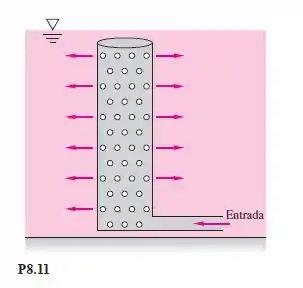
Uma central de energia descarrega água de refrigeração pelo distribuidor na Figura , que tem de diâmetro, de altura e é perfurado com orifícios de de diâmetro. O distribuidor simula uma fonte bidimensional? Em caso afirmativo, qual é a intensidade de fontes equivalente ?
Passo 1
E aí, tudo bem? Bora matar essa questão rapidinho!
O conceito do nosso problema é muito simples, como a quantidade furos é muito grande e podemos imaginar que eles estão espaçados igualmente, com fluxo igual. Então o distribuidor funciona como uma fonte bidimensional!
Passo 2
Pra matar de vez:
Onde:
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
O distribuidor funciona como uma fonte bidimensional!
Onde:
Exercícios de Livros Relacionados
Um escoamento incompressível bidimensional é definido por u = K y x 2 + y 2 v = K x x 2 + y 2 Em que K = constante. Esse escoamento é irrotacional? Em caso afirmativo, encontre seu potencial de veloci
Determine se as linhas de corrente de Stokes da equação 8.86 são ortogonais em todos os pontos às linhas equipotenciais de Stokes da equação (8.87), como ocorre no caso de coordenadas cartesianas e po
Estudamos a fonte (sumidouro) pontual e a fonte (sumidouro) bidimensional, isto é, em uma linha com profundidade infinita para dentro do papel. Faria sentido definir uma linha de sumidouros (fontes) d
Uma fonte pontual com vazão volumétrica Q = 30m 3 / s é imersa em uma corrente uniforme com 4 m/s de velocidade. Resulta um semicorpo de Rankine de revolução. Calcule (a) a distância da fonte ao ponto
O corpo de revolução de Rankine na figura abaixo tem 60 cm de comprimento e 30 cm de diâmetro. Quando imerso no túnel hidrodinâmico de baixa pressão como mostrado, a cavitação pode aparecer no ponto A