Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 98

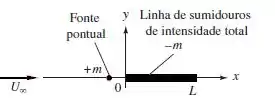
Estudamos a fonte (sumidouro) pontual e a fonte (sumidouro) bidimensional, isto é, em uma linha com profundidade infinita para dentro do papel. Faria sentido definir uma linha de sumidouros (fontes) de comprimento finito, como na figura abaixo? Em caso afirmativo, como você poderia estabelecer as propriedades matemáticas de tal linha finita de sumidouros? Quando combinada com uma corrente uniforme e uma fonte pontual de intensidade equivalente, como na figura abaixo, poderia surgir um formato de corpo fechado? Faça uma escolha e trace alguns desses possíveis formatos para vários valores do parâmetro adimensional .

Passo 1

E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos tem hora que o enunciado é mais assustador do que o que realmente a questão está pedindo.

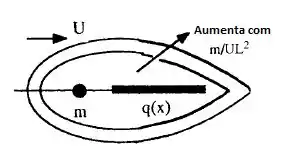
A resposta é “sim”, o sumidouro faz sentido e vai criar um corpo com um finalzinho mais pontiagudo, como se fosse uma gotinha!! Se q(x) for a força do sumidouro local, temos que e a forma do corpo é igual está na figura abaixo. E com o aumento do número adimensional a gente vai ter que essa gotinha ficaria cada mais e mais cheinha!!!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

É dado o potencial de velocidades em coordenadas polares no plano f 5 Br2cos(2u), sendo B uma constante. (a) Mostre que existe também uma função corrente. (b) Encontre a forma algébrica de c(r, u). (c

13 – Um pequeno tanque de peixes é aproximado por um formato de semicorpo, como mostra a Fig. 8.13. O ponto O, a 0,5 m de distância da borda esquerda do tanque, é uma fonte de água descarregando aprox

59 – Considere o escoamento não viscoso em torno de um cilindro com circulação nula, como na Fig. 8.14a (mostrada abaixo). Encontre (a) o ponto sobre a superfície frontal onde a aceleração do fluido a

PP8.3 – Considere água a 20°C escoando a 12 m/s em um canal. Um oval de Rankine cilíndrica de 40 cm de comprimento é posicionada paralelamente ao escoamento, onde a pressão estática da água é 120 kPa.

PP8.2 – Modifique o Problema PP8.1 para determinar a distribuição de fontes pontuais que aproxima um corpo de revolução de formato “0018”. Uma vez que não existe resultados publicados, simplesmente se