Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 97

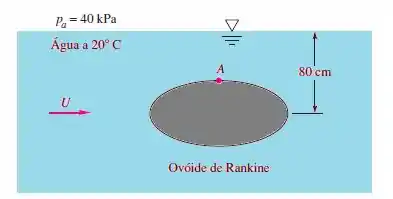
O corpo de revolução de Rankine na figura abaixo tem 60 cm de comprimento e 30 cm de diâmetro. Quando imerso no túnel hidrodinâmico de baixa pressão como mostrado, a cavitação pode aparecer no ponto A. Desprezando a formação de ondas superficiais, calcule a velocidade da corrente U para a qual aparece cavitação.

Passo 1

E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos é show de bola!

Primeiro de tudo vamos pegar as propriedades da água a 20°C!

ρ = 998   k g / m ³

p v a p o r = 2337   P a

Para um ovóide de Rankie de razão L R = 60 30 = 2 podemos interpolar na tabela 8.95 para encontrar que:

m U a 2 = 0,143

L a = 1,3735

Passo 2

Consequentemente podemos calcular que a = 30 1,3735 = 21,84   c m e de igual forma temos também que R = 0,687 a .

Portanto R = 15   c m

Passo 3

Continuando, podemos calcular m = 0,143 U a 2 , certo? Então com isso aqui já que temos o valor de a , podemos escrever m como uma função de U!!

m = 0,00682 U

De acordo com o livro, o cálculo da velocidade máxima pode ser dado como sendo:

U m á x = U + 2 m a r 3 2 = U + 2 ( 0,0068 U ) ( 0,2184 ) / [ 0,2184 2 + 0,15 2 ] 3 2 = 1,16 U

Passo 4

Agora, vamos escrever nossa equação de Bernoulli que vai nos permitir calcular U quando o ponto A estiver cavitando! E quando isso acontece? Quando a pressão nesse ponto for exatamente igual a pressão de vapor!!

p ∞ + ρ 2   U 2 + ρ g z ∞ = p A + ρ 2   V A 2 + ρ g z A

Onde V A = 1,16 U e que p ∞ = p a t m + ρ g z s u p e r f - z ∞

Lembrando que Z A = r = 0,15   m e z ∞ = 0

Fazendo isso, bora escrever na nossa equação de Bernoulli!!!

40000 + 998 9,81 0,8 - 0 U 2 + 0 = 2337 + 998 2 1,16 U 2 + 998 ( 9,81 ) ( 0,15 )

U = 16   m / s

Resposta

U = 16   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Water flows through a two-dimensional narrowing wedgeat 9.96 gal/min per meter of width into the paper(Fig. P4.72). If this inward fl ow is purely radial, find anexpression, in SI units, for (a) the s
Outside an inner, intense-activity circle of radius R, a tropical storm can be simulated by a polar-coordinate velocitypotential ϕ(r, θ) 5 UoR θ, where Uo is the wind velocity atradius R. (a) Determin
The velocity profi le for pressure-driven laminar flowbetween parallel plates (see Fig. 4.12b) has the form u 5C(h2 – y2), where C is a constant. (a) Determine if a streamfunction exists. (b) If so, f
A hole is placed in the front of a cylinder to measure thestream velocity of sea-level fresh water. The measuredpressure at the hole is 2840 lbf/ft2. If the hole is misalignedby 128 from the stream, a
A uniform stream, U∞ 5 4 m/s, approaches a Rankine ovalas in Fig. 8.13, with a 5 50 cm. Find the strength m of thesource–sink pair, in m2/s, which will cause the total lengthof the oval to be 250 cm.