Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 91
Uma chapa muito espessa, que tem difusividade térmica de e condutividade térmica igual a 20 W/(m · K), está inicialmente a uma temperatura uniforme de 325 °C. De repente, a sua superfície é exposta a um refrigerante a 15 °C para o qual o coeficiente de transferência de calor por convecção é de 100 W/(m² · K).
(a) Determine as temperaturas na superfície e a uma profundidade de 45 mm passados 3 min da exposição da chapa ao refrigerante.
(b) Calcule e represente graficamente os históricos de temperatura (0 ≤ t ≤ 300 s) em x = 0 e x = 45 mm para as seguintes variações paramétricas: (i) ; e (ii) k = 2, 20 e 200 W/(m · K).
Passo 1
Beleza! Nesse exercício, vamos modelar o problema como sendo um sólido semi-infinito com convecção na superfície, então a temperatura em um ponto, para um determinado intervalo de tempo, pode ser encontrada a partir da equação 5.63, que é dada por:
Então, como estamos interessados na temperatura da superfície no instante t = 3 min, então, teremos as seguintes variáveis para substituir na equação acima
Então, susbtituindo esses valores e os fornecidos no enunciado na equação acima, chegamos em:
Então, agora precisamos recorrer à tabela B.2 do apêndice B para encontrar o valor da função erro de Gauss, com isso, a nossa equação se torna:
Passo 2
Agora, repetindo o cálculo do passo 1, só que para a profundidade x = 45 mm, temos:
Então, agora precisamos recorrer à tabela B.2 do apêndice B para encontrar o valor da função erro de Gauss, com isso, a nossa equação se torna:
Passo 3
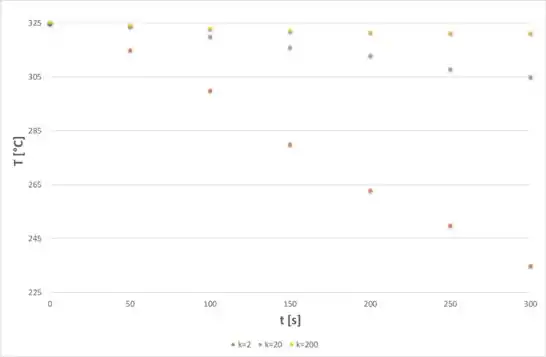
Agora, para a letra (b), vamos utilizar a mesma equação utilizada nos passos 1 e 2 para se obter a temperatura em um determinado ponto e em determinado instante de tempo, a diferença agora é que teremos que calcular para os dois valores de x novamente, na superfície e 45 mm abaixo, só que também teremos que calcular esses valores no intervalo de tempo de 0 até 300 segundos, para os diferentes valores de difusividade térmica fornecidos e depois para diferentes valores de condutividade. Primeiramente vamos calcular para o caso onde teremos condutividade térmica constante, mas variando a difusividade, com isso, na superfície, obtemos o seguinte gráfico:
Agora, para o mesmo caso, só que em x = 45 mm, temos o seguinte comportamento:
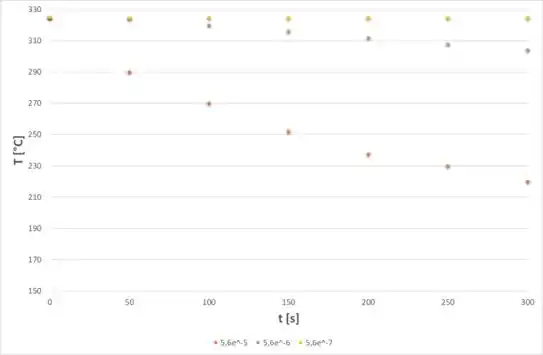
Passo 4
Agora nós vamos manter a difusividade constante em e variar a condutividade térmica do material. Então, fazendo a análise primeiramente para a superfície, temos:
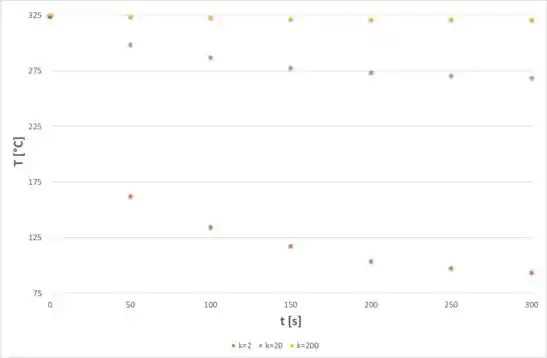
E, agora, para a profundidade x = 45 mm, temos:
