Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 11.Exercício - Ex. 27
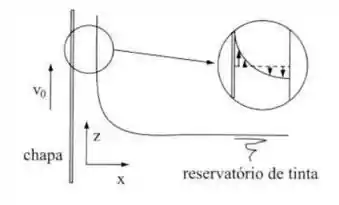
Uma chapa fina deve passar de forma contínua num banho de tinta contido num reservatório, como mostra a figura. Em regime permanente, o diagrama de velocidades bidimensional é tal que, numa seção, a vazão é nula, já que parte da tinta sobe arrastada pela chapa e parte retorna por gravidade, mantendo a espessura constante. Como a velocidade da chape é baixa, admite-se que o atrito com o ar é desprezível. Determinar
- A expressão do diagrama de velocidades
- A velocidade de subida da chapa para que a espessura da camada de tinta seja
Dados:
Passo 1
Primeiro, vamos considerar que o regime é permanente. Além disso, consideraremos que o movimento é unicamente no eixo , assim, . A questão também nos afirma que a velocidade em é função apenas de , então . Por fim, já que a espessura é constante, e a pressão é igual a pressão atmosférica, então
Com isso, a equação 11.40 de navier-stokes se reduz para:
Podemos simplificar para um integral total:
Integrando duas vezes temos:
Passo 2
Na superfície de contato com a chapa (), a velocidade do fluido é igual à velocidade da chapa:
Analogamente, no ponto de maior espessura, onde não há contato com chapa, a velocidade é máxima. E no ponto de velocidade máxima, a derivada é zero:
Assim, a expressão do diagrama de velocidades é:
Passo 3
Item B)
Sabemos que a vazão de fluido é zero, e podemos calcular a vazão partindo da velocidade. Vamos usar isso para calcular a velocidade de subida da chapa.
A área é igual ao comprimento da chapa, vezes a espessura de fluido. Os limites vão de zero até a espessura total do fluido