Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 2.Problemas - Ex. 42
Uma chapa plana fina de dimensões é puxada horizontalmente com velocidade de sobre uma camada de óleo de de espessura entre duas chpas planas, uma estacionária e a outra movendo-se com a velocidade constante de , como mostrado na Figura P2-32. A viscosidade dinâmica do óleo é . Considerando que a velocidade de cada camada de óleo varie linearmente, trace o perfil da velocidade e determine o ponto em que a velocidade do óleo seja nula e determine a força que precisa ser aplicada sobre a chapa para manter o movimento.
Passo 1
O perfil de velocidade em cada camada de óleo em relação à parede fixa é como mostrado na figura abaixo:
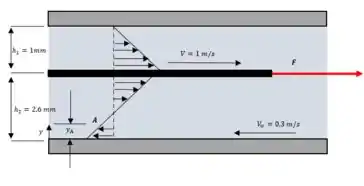
Onde temos que o ponto de velocidade zero é indicado pelo ponto A.
E sua distância da placa inferior é determinada por considerações geométricas (a semelhança dos dois triângulos na camada inferior de óleo) como sendo:
Passo 2
As magnitudes das forças de cisalhamento que atuam nas superfícies superior e inferior da placa são:
Passo 3
Portanto, observando que ambas as forças de cisalhamento estão na direção oposta ao movimento da placa, a força é determinada a partir de um equilíbrio de força, temos que:
Resposta
Logo temos que:
O ponto em que a velocidade do óleo seja nula é:
A força que precisa ser aplicada sobre a chapa para manter o movimento é: