Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 88

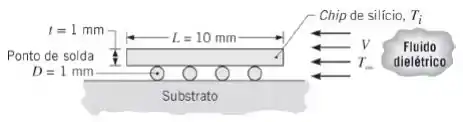
Um chip de silício ( k   =   150   W / ( m   ·   K ) ,   ρ   =   2300   k g / m 3   e c p   =   700   J / ( k g   ·   K ) ) , com 10   m m de lado e 1   m m de espessura, está ligado ao substrato por pontos de solda ( k   =   40   W / ( m   ·   K ) ,   ρ   =   10.000   k g / m 3   e   c p   =   150   J / ( k g   ·   K ) ) com 1   m m de diâmetro. Durante um teste acelerado de estresse térmico, o sistema é exposto ao escoamento de um fluido dielétrico ( k   =   0,064   W / ( m   ·   K ) ,   v   =   10 - 6   m 2   / s ,   P r   =   25 ) . Como uma primeira aproximação, tome as superfícies superior e inferior do chip como placas planas em um escoamento paralelo e turbulento, e admita que o substrato e a superfície inferior do chip tenham influência desprezível no escoamento sobre os pontos de solda. Também suponha contato pontual entre o chip e a solda, desta forma desprezando a transferência de calor por condução entre os componentes.

(a) O teste de estresse inicia com os componentes na temperatura ambiente ( T i   =   20 ° C ) e prossegue com o aquecimento pelo fluido a T ∞   =   80 ° C . Sendo a velocidade do fluido V   =   0,2   m / s , determine a razão entre as constantes de tempo do chip e do ponto de solda. Qual componente responde mais rapidamente ao processo de aquecimento?

(b) O estresse térmico agindo sobre o ponto de solda é proporcional à diferença de temperaturas entre o chip e a solda. Qual é a diferença de temperaturas 0,25   s após o início do aquecimento?

Passo 1

Nessa questão nós temos a temperatura inicial, as dimensões e as propriedades dos conectores de chip e solda. Além da velocidade, temperatura e propriedades do líquido.

Com isso precisamos encontrar a razão de constantes de tempo (chip para solda) e a diferença de temperatura entre o chip e a solda após 0,25 s de aquecimento. Partiu?!

Passo 2

Para resolver essa questão vamos assumir que:

(1) As esferas e lascas de solda são espacialmente isotérmicas;

(2) A transferência de calor é desprezível pelos lados da lasca;

(3) As superfícies superior e inferior do cavaco agem como placas planas em fluxo paralelo turbulento;

(4) A transferência de calor das esferas de solda pode ser aproximado como o de uma esfera isolada;

(5) As propriedades são constantes.

Na letra (a) queremos encontrar a razão entre as constantes de tempo do chip e do ponto de solda. A constante de tempo térmico é

  τ t = ρ V c h - A s      

Então,

τ t , c h τ t , s l d = ρ c c h ( L 2 t ) 2 h - c h L 2 h - s l d π D 2 ρ c s l d π D 3 6 = 3 t D ρ c c h ρ c s l d h - s l d h - c h

O coeficiente de convecção para o chip pode ser obtido com A   =   0 , com,

R e L = V L v = 0,2 m / s × 0,0 1 m 10 - 6   m 2 / s = 20 00

Então,

h - c h = 0,064 W m . K 0,01 m 0,037 2000 4 5 25 1 3 = 302 W m 2 . K

Passo 3

O coeficiente de convecção para a solda pode ser obtido com,

R e D = V D v = 0,2 m / s × 0,00 1 m 10 - 6   m 2 / s = 20 0

Desprezando o efeito da razão de viscosidade,

h s l d - = 0,0 64 W m . K 0,001 m 2 + 0,4 2 00 + 0,06 × 2 00 2 3 × 25 0,4 = 1916   W / m 2 . K

Então,

τ t , c h τ t , s l d = 3 2300 k g m 3 × 700 J k g . K 100 00 k g m 3 × 15 0 J k g . K 1916   W / m 2 . K 302   W / m 2 . K = 20,4

Sendo assim, a solda responde muito mais rapidamente ao aquecimento por convecção.

Passo 4

Na letra (b) queremos a diferença de temperaturas 0,25   s após o início do aquecimento. A diferença de temperatura entre o chip e a solda pode ser expressa como:

T c h - T s l d = T i - T ∞ exp ⁡ - 2 h - ρ   c   t c h t - exp ⁡ - 6 h - ρ   c   D s l d t

Substituindo os valores,

T c h - T s l d = 60 ° C exp ⁡ - 604   W / m 2 . K 1610   J / m 2 . K 0,25 s - exp ⁡ - 11496   W / m 2 . K 1 50 0   J / m 2 . K 0,25 s

T c h - T s l d = 60 ° C 0,910 - 0,147 = 45,8 ° C

Resposta

  1. A solda responde muito mais rapidamente ao aquecimento por convecção.
  2. T c h - T s l d = 45,8 ° C
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ar a 20°C (1 atm) está escoando sobre uma esfera de diâmetro de 5 cm a uma velocidade de 3,5 m/s. Considerando que a temperatura de superfície da esfera é constante a 80°C, determine (a) o coeficiente
Uma bola de aço inoxidável (ρ = 8,055 kg/m³, Cp= 480 J/kg.K) de diâmetro D = 15 cm é retirado do forno a uma temperatura uniforme de 350°C. A bola é, então submetida ao escoamento de ar a 1 atm de pre
Um aerofólio metálico de seção transversal elíptica tem massa de 50 kg, área superficial de 12 m2 e calor específico de 0,50 kJ/kg.K. O aerofólio foi submetido a escoamento de ar a 1 atm, 25°C e 5 m/s
Usando cilindro, esfera e cubo como exemplos, mostre que a taxa de transferência de calor é inversamente preporcional à dimensão nominal do objeto. Ou seja, a transferência de calor por unidade de áre
54 – Uma pessoa média gera calor a uma taxa de 84W enquanto descansa. Pressupondo que 1 / 4 desse calor seja perdido pela cabeça e ignorando a radiação, determine a temperatura média da superfície da