Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 6.Problemas - Ex. 68

Usando cilindro, esfera e cubo como exemplos, mostre que a taxa de transferência de calor é inversamente preporcional à dimensão nominal do objeto. Ou seja, a transferência de calor por unidade de área aumenta à medida que o tamanho do objeto diminui.

Passo 1

A fórmula geral de fluxo de calor é:

F l u x o = q ˙ A s = - k ∂ T ∂ y

Em que A s é a área superficial e y é a direção em que ocorre a transferência de calor.

O que vamos fazer é escrever esta mesma fórmula para as três geometrias (cilindro, esfera e cubo) para demonstrar que o fluxo é inversamente proporcional às dimensões nominais do objeto ( r para cilindro e esfera, L para o cubo).

Vamos começar pela esfera:

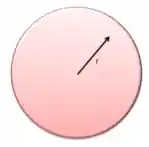
Em uma esfera a transferência de calor ocorre na direção r . Além disso, sabemos que a área superficial de uma esfera é A s = 4 π r 2 . Vamos substituir essas duas informações na equação geral:

q ˙ 4 π r 2 = - k ∂ T ∂ r  

q ˙ 4 π r 2 ∂ r = - k ∂ T

Imaginando que a transferência de calor ocorra de um raio r 1 até r 2 , com temperaturas T 1 e T 2 , respectivamente, vamos integrar os dois lados da equação:

∫ r 1 r 2 q ˙ 4 π r 2 ∂ r = ∫ T 1 T 2 - k ∂ T

- q ˙ 4 π 1 r r 1 r 2 = - k ( T 2 - T 1 )

q ˙ = 4 π k T 2 - T 1 1 r 2 - 1 r 1

q ˙ = 4 π r 1 r 2 k T 2 - T 1 r 1 - r 2

Vamos dividir essa equação pela área da esfera ( 4 π r 2 2 ) para transformar q ˙ em fluxo:

F l u x o = q 4 π r 2 2 ˙ = 4 π r 1 r 2 k T 2 - T 1 4 π r 2 2 r 1 - r 2

F l u x o = r 1 r 2 k T 2 - T 1 r 1 - r 2

Pela equação podemos ver que quanto maior o tamanho da esfera (ou seja, quanto maior for r 2 ), menor será o fluxo. Portanto, o fluxo é inversamente proporcional ao tamanho da esfera.

Passo 2

Vamos agora pensar o mesmo problema para uma geometria cilíndrica.

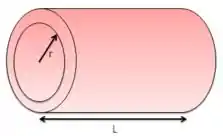
Em um cilindro a transferência de calor ocorre na direção r . Além disso, sabemos que a área superficial de um cilindro é A s = 2 π r L . Vamos substituir essas duas informações na equação geral:

q ˙ 2 π r L = - k ∂ T ∂ r  

q ˙ 2 π r L ∂ r = - k ∂ T

Imaginando que a transferência de calor ocorra de um raio r 1 até r 2 , com temperaturas T 1 e T 2 , respectivamente, vamos integrar os dois lados da equação:

∫ r 1 r 2 q ˙ 2 π r L ∂ r = ∫ T 1 T 2 - k ∂ T

q ˙ 2 π L ln ⁡ r r 1 r 2 = - k ( T 2 - T 1 )

q ˙ = - 2 π k L T 2 - T 1 ln ⁡ r 2 - ln ⁡ r 1

q ˙ = - 2 π k L T 2 - T 1 ln ⁡ r 2 r 1

Vamos dividir essa equação pela área da esfera ( 2 π r 2 L ) para transformar q ˙ em fluxo:

F l u x o = q 2 π r 2 L ˙ = - 2 π k L T 2 - T 1 2 π r 2 L ln ⁡ r 2 r 1

F l u x o = - 1 r 2 k T 2 - T 1 ln ⁡ r 2 r 1

Pela equação podemos ver que quanto maior o tamanho do cilindro (ou seja, quanto maior for r 2 ), menor será o fluxo. Portanto, o fluxo é inversamente proporcional ao tamanho do cilindro.

Passo 3

Por fim, vamos considerar a transferência de calor unidimensional em um cubo.

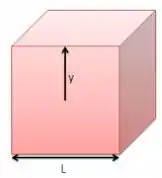
Em um cubo, a transferência de calor ocorre na direção y . Além disso, sabemos que a área superficial de um lado do cubo é A s = y 2 . Vamos substituir essas duas informações na equação geral:

q ˙ y 2 = - k ∂ T ∂ y  

q ˙ y 2 ∂ y = - k ∂ T

Imaginando que a transferência de calor ocorra de determinado y 1 até y 2 , com temperaturas T 1 e T 2 , respectivamente, vamos integrar os dois lados da equação:

∫ y 1 y 2 q ˙ y 2 ∂ y = ∫ T 1 T 2 - k ∂ T

- q ˙ 1 y y 1 y 2 = - k ( T 2 - T 1 )

q ˙ = k T 2 - T 1 1 y 2 - 1 y 1

q ˙ = y 1 y 2 k T 2 - T 1 y 1 - y 2

Vamos dividir essa equação pela área de um lado do cubo ( y 2 2 ) para transformar q ˙ em fluxo:

F l u x o = q y 2 2 ˙ = y 1 y 2 k T 2 - T 1 y 2 2 y 1 - y 2

F l u x o = y 1 y k T 2 - T 1 y 1 - y 2

Pela equação podemos ver que quanto maior o tamanho do cubo (ou seja, quanto maior for y 2 ), menor será o fluxo. Portanto, o fluxo é inversamente proporcional ao tamanho do cubo.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Leitos recheados de partículas esféricas podem ser sinterizados a altas temperaturas para formar espumas rígidas permeáveis. Uma folha de espuma com espessura t = 10 mm é formada por esferas de bronze
Considere a medida de temperatura em uma corrente de gás com a junta de termopar descrita no Problema 7.86 ( D=2m m ,ε=0,60 ) . Se a velocidade e a temperatura do gás são de 3m / s e 500 ° C , respect
Uma esfera de cobre puro, com diâmetro de 15m m e uma emissividade de 0,5 , está suspensa em um grande forno com as paredes a uma temperatura uniforme de 600 ° C . Ar escoa ao redor da esfera a uma te
Para as condições fornecidas no Problema 7.80, quais são a velocidade terminal e a altura do tanque se óleo de motor a 300K for usado como refrigerante no lugar da água?
Revestimentos de alumínio altamente refletivos podem ser formados na superfície de um substrato pela aspersão da superfície com gotas de alumínio fundido. As gotas são descarregadas de um injetor, des