Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 67
A cidade de Englewood, no Colorado, é abastecida com água do South Platte River, na elevação de 1610 m [54]. A água é bombeada para reservatórios de armazenagem na elevação de 1620 m. O diâmetro interno da tubulação de aço é 68,5 cm; seu comprimento é 1770 m. A instalação foi projetada para uma capacidade (vazão) inicial de 3200 m³/h e uma capacidade futura de 3900 m³/h. Calcule e trace a curva de resistência do sistema. Especifique um sistema apropriado de bombeamento. Estime a potência de bombeamento requerida para operação em regime permanente, para ambas as vazões, inicial e futura.
Passo 1
Beleza! Vamos começar o exercício aplicando o equilíbrio de energia para o sistema entre O rio South Platte River (ponto 1) e os reservatórios (ponto 2), então, temos:
Como sabemos que na entrada temos , podemos cancelar os termos de pressão. Sabemos também que podemos considerar pois o rio e os reservatórios são de grandes dimensões. Dessa forma, a equação se torna:
E, sabemos que a perda de carga, contendo perdas distribuídas e localizadas, pode ser escrita como:
Passo 2
Agora com essa velocidade, conseguimos encontrar o número de Reynolds, para isso, vamos pegar alguns dados da Tabela A.7 do livro, inclusive uns que usaremos mais tarde:
Agora, para encontrar o fator de atrito, precisamos primeiro pegar o dado referente à rugosidade da tubulação, que se encontra na tabela a seguir presente no capítulo 8:
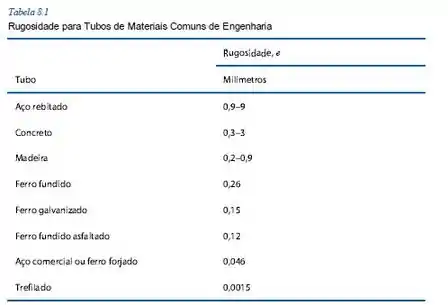
Então, como temos aço comercial, teremos . Então agora podemos usar a equação de Colebrook e descobrir o valor do fator de atrito:
Passo 3
Agora vamos voltar à equação do equilíbrio de energia do passo 1:
E substituir a expressão encontrada para a perda de carga específica no passo 1:
Agora precisamos recorrer às tabelas 8.2 e 8.4 e ao diagrama de expansão/contração apresentados no livro para encontrar os coeficientes de perda:
Nesse exercício, não foi mencionada a utilização de nenhum acessório, então temos:
Não temos nenhuma perda na entrada também, mas vamos considerar uma saída brusca para o sistema, uma vez que a tubulação pequena descarrega em um grande reservatório, dessa forma, temos:
Então, agora, substituindo todos os valores conhecidos na equação de energia, temos:
Sabemos que a altura de carga específica da bomba pode ser escrita como:
Então, substituindo essa expressão na equação anterior, temos:
Passo 4
Então, será esse gráfico que precisamos plotar, só que em função da vazão. Então, escrevendo a velocidade em função da vazão, temos:
Substituindo essa expressão na equação anterior, temos:
Então como temos o fator de atrito dependendo da vazão, teremos que chutar valores de vazão, calcular a velocidade e depois calcular o valor de atrito para então encontrar o valor de . Fazendo isso, chegamos no seguinte gráfico:
Passo 5
Para encontrar um sistema apropriado de bombeamento, precisamos converter a vazão para , então, temos:
Dessa forma, para essa vazão e para a altura de carga correspondente encontrada no gráfico, que será:
Então, com o diagrama de seleção de bombas a seguir, temos:
Podemos ver que uma só bomba não atenderia a vazão encontrada, então, pegando duas bombas 10AE14 (G) em paralelo, atendemos aos requisitos de projeto.
Passo 6
Agora para encontrar a potência de bombeamento nos dois casos, iremos utilizar a equação da potência da bomba, dada por:
Para uma eficiência de 90% e as condições:
Temos:
E, para a condição posterior de:
Temos: