Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 8

O campo de velocidade, para uma fonte plana localizada a uma distância h = 1   m acima de uma parede infinita alinhada ao longo do eixo x , é dado por:

V → = q 2 π x 2 + y - h 2 x i → + y - h j → + q 2 π x 2 + y + h 2 x i → + y + h j →

Em que q = 2   m 3 / s / m . A massa específica do fluido é 1000 kg/m³ e as forças de campo são desprezíveis. Deduza expressões para a velocidade e aceleração de uma partícula fluida movendo-se ao longo da parede, e trace um gráfico de x = 0 a x = + 10 h . Verifique se a velocidade e a aceleração normais à parede são iguais a zero. Trace um gráfico do gradiente de pressão ∂ p / ∂ x ao longo da parede. O gradiente de pressão ao longo da parede é adverso (ele opõe-se ao movimento do fluido), ou não?

Passo 1

Tá legal! Vamos começar esse exercício escrevendo as componentes de velocidade u e v através dos dados do enunciado, então, temos:

u = q x 2 π x 2 + y - h 2 + q x 2 π x 2 + y + h 2

v = q y - h 2 π x 2 + y - h 2 + q y + h 2 π x 2 + y + h 2

Agora, sabemos que a equação da aceleração é dada por:

a → = u ∂ V → ∂ x + v ∂ V → ∂ y + w ∂ V → ∂ z + ∂ V → ∂ t

No nosso caso, não temos nenhum termo da velocidade dependendo do tempo e nem da direção z , então nossa equação se torna:

a → = u ∂ V → ∂ x + v ∂ V → ∂ y

Passo 2

Então vamos calcular as componentes da aceleração em x e y :

a x = u ∂ u ∂ x + v ∂ u ∂ y = u ∂ ∂ x q x 2 π x 2 + y - h 2 + q x 2 π x 2 + y + h 2 + v ∂ ∂ y q y - h 2 π x 2 + y - h 2 + q y + h 2 π x 2 + y + h 2

Vamos calcular um termo de cada vez, então temos:

u ∂ u ∂ x = u ∂ ∂ x q x 2 π x 2 + y - h 2 + q x 2 π x 2 + y + h 2

u ∂ u ∂ x = u q 2 π x 2 + y - h 2 - q x 4 π x 2 π x 2 + y - h 2 2 + q 2 π x 2 + y + h 2 - q x 4 π x 2 π x 2 + y + h 2 2

u ∂ u ∂ x = q x 2 π x 2 + y - h 2 + q x 2 π x 2 + y + h 2 q 2 π x 2 + y - h 2 - q x 4 π x 2 π x 2 + y - h 2 2 + q 2 π x 2 + y + h 2 - q x 4 π x 2 π x 2 + y + h 2 2

Agora na direção y :

v ∂ u ∂ y = v ∂ ∂ y q x 2 π x 2 + y - h 2 + q x 2 π x 2 + y + h 2

v ∂ u ∂ y = v 0 2 π x 2 + y - h 2 - q x 4 π y - h 2 π x 2 + y - h 2 2 + 0 2 π x 2 + y + h 2 - q x 4 π y + h 2 π x 2 + y + h 2 2

v ∂ u ∂ y = q y - h 2 π x 2 + y - h 2 + q y + h 2 π x 2 + y + h 2 - q x 4 π y - h 2 π x 2 + y - h 2 2 + - q x 4 π y + h 2 π x 2 + y + h 2 2

Essas serão as componentes da velocidade em x , não vamos colocar todos os termos na mesma equação pois a visualização ficaria prejudicada.

Passo 3

Agora vamos repetir o processo do passo 2 para a aceleração em y , então, temos:

a y = u ∂ v ∂ x + v ∂ v ∂ y = u ∂ ∂ x q y - h 2 π x 2 + y - h 2 + q y + h 2 π x 2 + y + h 2 + v ∂ ∂ y q y - h 2 π x 2 + y - h 2 + q y + h 2 π x 2 + y + h 2

Vamos calcular um termo de cada vez, então temos:

u ∂ v ∂ x = u ∂ ∂ x q y - h 2 π x 2 + y - h 2 + q y + h 2 π x 2 + y + h 2

u ∂ v ∂ x = u ( 0 ) x 2 + y - h 2 - q ( y - h ) ( 4 π x ) 2 π x 2 + y - h 2 2 + ( 0 ) x 2 + y - h 2 - q ( y + h ) ( 4 π x ) 2 π x 2 + y + h 2 2

u ∂ v ∂ x = q x 2 π x 2 + y - h 2 + q x 2 π x 2 + y + h 2 - q ( y - h ) ( 4 π x ) 2 π x 2 + y - h 2 2 + - q ( y + h ) ( 4 π x ) 2 π x 2 + y + h 2 2

Agora na direção y :

v ∂ v ∂ y = v ∂ ∂ y q y - h 2 π x 2 + y - h 2 + q y + h 2 π x 2 + y + h 2

v ∂ v ∂ y = v q 2 π x 2 + y - h 2 - q ( y - h ) 4 π y - h 2 π x 2 + y - h 2 2 + q 2 π x 2 + y + h 2 - q ( y + h ) 4 π y + h 2 π x 2 + y + h 2 2

v ∂ v ∂ y = q y - h 2 π x 2 + y - h 2 + q y + h 2 π x 2 + y + h 2 - q x 4 π y - h 2 π x 2 + y - h 2 2 + - q x 4 π y + h 2 π x 2 + y + h 2 2

Passo 4

Tá legal, então, como queremos analisar condições ao longo da parede, onde temos y = 0 , então as velocidades se tornam:

u = q x 2 π x 2 + y - h 2 + q x 2 π x 2 + y + h 2

u = q x 2 π x 2 + 0 - h 2 + q x 2 π x 2 + 0 + h 2 → u = q x π x 2 + h 2

v = q y - h 2 π x 2 + y - h 2 + q y + h 2 π x 2 + y + h 2

v = q 0 - h 2 π x 2 + 0 - h 2 + q 0 + h 2 π x 2 + 0 + h 2 → v = 0

E, as acelerações serão:

u ∂ u ∂ x = q x 2 π x 2 + y - h 2 + q x 2 π x 2 + y + h 2 q 2 π x 2 + y - h 2 - q x 4 π x 2 π x 2 + y - h 2 2 + q 2 π x 2 + y + h 2 - q x 4 π x 2 π x 2 + y + h 2 2

u ∂ u ∂ x = q x 2 π x 2 + 0 - h 2 + q x 2 π x 2 + 0 + h 2 q 2 π x 2 + 0 - h 2 - q x 4 π x 2 π x 2 + 0 - h 2 2 + q 2 π x 2 + 0 + h 2 - q x 4 π x 2 π x 2 + 0 + h 2 2

u ∂ u ∂ x = q x π x 2 + h 2 q 2 π x 2 + h 2 - q x 4 π x 2 π x 2 + h 2 2 + q 2 π x 2 + h 2 - q x 4 π x 2 π x 2 + h 2 2

v ∂ u ∂ y = q y - h 2 π x 2 + y - h 2 + q y + h 2 π x 2 + y + h 2 - q x 4 π y - h 2 π x 2 + y - h 2 2 + - q x 4 π y + h 2 π x 2 + y + h 2 2

v ∂ u ∂ y = q 0 - h 2 π x 2 + 0 - h 2 + q 0 + h 2 π x 2 + 0 + h 2 - q x 4 π 0 - h 2 π x 2 + 0 - h 2 2 + - q x 4 π 0 + h 2 π x 2 + 0 + h 2 2

v ∂ u ∂ y = 0 - q x 4 π - h 2 π x 2 + - h 2 2 + - q x 4 π h 2 π x 2 + h 2 2 → v ∂ u ∂ y = 0

Então a aceleração em x será:

a x = u ∂ u ∂ x + v ∂ u ∂ y = q x π x 2 + h 2 q 2 π x 2 + h 2 - q x 4 π x 2 π x 2 + h 2 2 + q 2 π x 2 + h 2 - q x 4 π x 2 π x 2 + h 2 2

Passo 5

Agora, substituindo o valor de y = 0 na aceleração na direção y , temos:

u ∂ v ∂ x = q x 2 π x 2 + y - h 2 + q x 2 π x 2 + y + h 2 - q ( y - h ) ( 4 π x ) 2 π x 2 + y - h 2 2 + - q ( y + h ) ( 4 π x ) 2 π x 2 + y + h 2 2

u ∂ v ∂ x = q x 2 π x 2 + 0 - h 2 + q x 2 π x 2 + 0 + h 2 - q ( 0 - h ) ( 4 π x ) 2 π x 2 + 0 - h 2 2 + - q ( 0 + h ) ( 4 π x ) 2 π x 2 + 0 + h 2 2

u ∂ v ∂ x = q x π x 2 + h 2 0 → u ∂ v ∂ x = 0

E, o segundo termo será:

v ∂ v ∂ y = q y - h 2 π x 2 + y - h 2 + q y + h 2 π x 2 + y + h 2 - q x 4 π y - h 2 π x 2 + y - h 2 2 + - q x 4 π y + h 2 π x 2 + y + h 2 2

v ∂ v ∂ y = q 0 - h 2 π x 2 + 0 - h 2 + q 0 + h 2 π x 2 + 0 + h 2 - q x 4 π 0 - h 2 π x 2 + 0 - h 2 2 + - q x 4 π 0 + h 2 π x 2 + 0 + h 2 2

v ∂ v ∂ y = 0 0 → v ∂ v ∂ y = 0

Então, a aceleração em y será:

a y = u ∂ v ∂ x + v ∂ v ∂ y = 0 + 0 → a y = 0

Passo 6

Agora, para encontrar o gradiente de pressão, temos a seguinte equação:

ρ D V → D t = ρ g → - ∇ p

Como não temos velocidade e nem aceleração em y , então não temos gradiente de pressão nessa direção na parede, então, a equação do gradiente de pressão em x se resume à:

ρ D u D x = - ∂ p ∂ x → ∂ p ∂ x = - ρ D u D x

No entanto, nós já encontramos o termo D u / D x lá no passo 4, pois esse termo nada mais é do que a aceleração na direção x , então a equação para o gradiente de pressão se torna:

∂ p ∂ x = - ρ q 2 π x 2 + h 2 - q x 4 π x 2 π x 2 + h 2 2 + q 2 π x 2 + h 2 - q x 4 π x 2 π x 2 + h 2 2

Passo 7

Agora vamos plotar todos os gráficos pedidos no enunciado, a velocidade será:

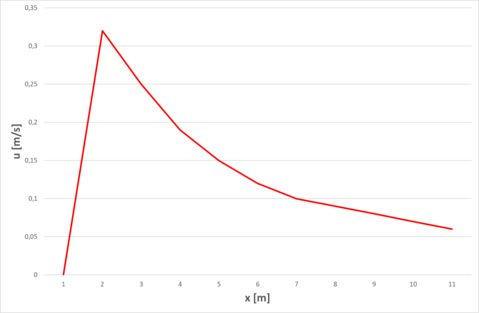
A aceleração será:

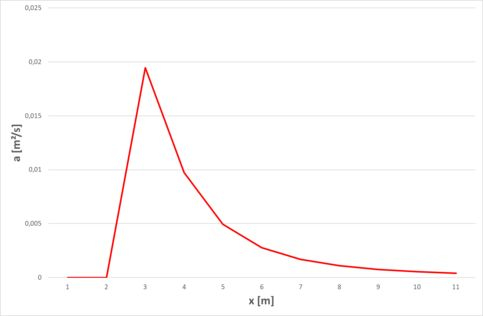
E, por fim, o gradiente de pressão:

Resposta

u = q x π x 2 + h 2 ;   v = 0

a x = q x π x 2 + h 2 q 2 π x 2 + h 2 - q x 4 π x 2 π x 2 + h 2 2 + q 2 π x 2 + h 2 - q x 4 π x 2 π x 2 + h 2 2 ;   a y = 0

∂ p ∂ x = - ρ q 2 π x 2 + h 2 - q x 4 π x 2 π x 2 + h 2 2 + q 2 π x 2 + h 2 - q x 4 π x 2 π x 2 + h 2 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Estime a velocidade à qual você precisaria nadar na água à temperatura ambiente para estar em regime de escoamento lento. (Uma estimativa da ordem de grandeza será suficiente.) Discuta.
Na derivação de uma equação de Bernoulli para regiões de escoamento sem viscosidade, usamos a identidade vetorial: V → ⋅ ∇ → V → = ∇ → V 2 2 - V → x( ∇ →xV → ) Mostre que essa identidade vetorial é sa
Combine os resultados dos Problemas 10-26 e 10-28 para mostrar que para um mancal de bloco deslizante bidimensional, o gradiente de pressão d P / d x está relacionado com a altura h do espaçamento por
Considere novamente o mancal de bloco deslizante do Problema 10-23. Faça uma análise de ordem de grandeza na equação do momento y e escreva a forma final da equação do momento y . (Sugestão: Você prec
Um bom nadador nada 100 m em aproximadamente 1 minuto. Se o corpo do nadador tiver 1,8 m de comprimento, quantos comprimentos equivalentes ao seu corpo ele nada por segundo? Repita o cálculo para o es