Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 14.Problemas - Ex. 7
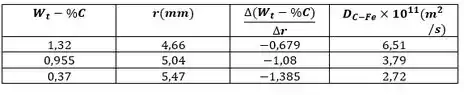
Um cilindro oco de ferro, com de comprimento, está exposto a um gás de carburização (uma mistura de e ) a nas suas superfícies interna e externa com raios e , respectivamente. Considere condições de regime estacionário, nas quais o carbono se difunde da superfície interna da parede de ferro para a superfície externa e a quantidade total do transporte de de carbono em . A variação da composição de carbono (porcentagem em massa de carbono) com o raio é mostrada na tabela em raios selecionados.
(a) Iniciando com a lei de Fick e com a hipótese de coeficiente de difusão constante, , mostre que é uma constante. Esboce a concentração mássica de carbono, ), como uma função de para tal processo difusivo.
(b) A tabela anterior corresponde a uma distribuição de concentrações mássicas de carbono medidas. é uma constante nesse processo difusivo? Se não, aumenta ou diminui com o aumento da concentração de carbono?
(c) Usando os dados experimentais, calcule e mostre em uma tabela para as composições de carbono selecionadas.
Passo 1
Nessa questão nós temos que as superfícies interna e externa de um cilindro de ferro de de comprimento são expostas a um gás de carburação (misturas de e ).
Foram fornecidos dados experimentais observados sobre a variação da composição de carbono (peso de carbono) no ferro a em função do raio. E com isso, vamos encontrar fazer o esboço da densidade mássica de carbono, em função de para esse processo de difusão.
Além disso, vamos criar um gráfico para os dados experimentais e determinar se o para este processo de difusão é constante, aumenta ou diminui com o aumento da densidade de massa. Por fim, vamos calcular e fazer uma tabela do para composições de carbono selecionadas ao longo do intervalo do experimento. Ufa! Vamos lá!
Passo 2
Para resolver essa questão vamos assumir:
(1) Condições de estado estacionário;
(2) Difusão radial unidimensional em meio estacionário;
(3) Concentração total uniforme.
Para o sistema de coordenadas radial (cilíndrico) unidimensional, a lei de Fick é:
Onde,
Para condições de estado estacionário, é constante e, se for constante, o produto,
Deve ser uma constante.
Passo 3
Usando a relação diferencial,
Temos que,
De modo que em um gráfico de é uma linha reta.
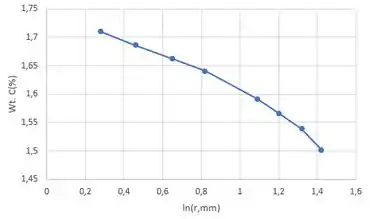
Passo 4
Para determinar se o é uma constante para o processo de difusãoe xperimental, os dados são representados em uma coordenada
Como o gráfico não é linear, o não é uma constante. A partir do tratamento da parte (a), se o não for uma constante, então:
Deve ser constante. Com isso, concluímos que o será menor na posição radial, onde o gradiente é maior. Portanto, esperamos que o aumente com o aumento do teor de carbono.
Passo 5
O gradiente da fração de massa é determinado em três locais e a lei de Fick é usada para calcular o coeficiente de difusão,
Onde a vazão mássica é,
E,
Sendo a densidade do ferro. Os resultados dessa análise geram,
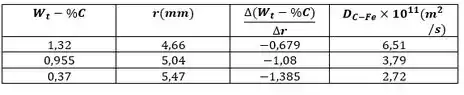
Resposta
(a)
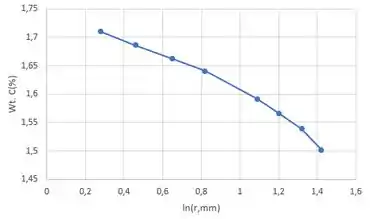
(b) Deve ser constante. Com isso, concluímos que o será menor na posição radial, onde o gradiente é maior. Portanto, esperamos que o aumente com o aumento do teor de carbono.
(c)
