Os componentes de uma placa de circuitos vertical quadrada, com de lado, dissipam . A superfície posterior é isolada termicamente e a superfície frontal está exposta ao ar quiescente a .

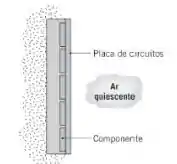
Admitindo um fluxo térmico na superfície uniforme, qual é a temperatura máxima na placa? Qual é a temperatura da placa para uma condição de superfície isotérmica?

Para resolver essa questão vamos assumir que ou é uniforme e o ar ambiente é quieto. Para o caso uniforme do fluxo de calor, o fluxo de calor é:

Onde,

E,

A temperatura máxima na placa ocorrerá em e,

O coeficiente médio de transferência de calor é estimado a partir de uma correlação vertical ( uniforme) com base na diferença de temperatura . Aqui será necessário um procedimento iterativo no qual vamos seguir os seguintes passos:

1. Assumir um valor de e encontrar ;
2. Avaliar o número de Rayleigh, e usar a correlação apropriada para estimar ;
3. Encontrar o valor calculado de
4. Repetir este procedimento até o valor calculado para estar próximo de , o fluxo de calor necessário.

Para avaliar as propriedades para a correlação, vamos usar a temperatura do filme,

Interação 1: Assumindo , temos,

E o número de Rayleigh é,

Como , o fluxo da camada limite é laminar então podemos usar a seguinte correlação:

Assim, o fluxo de calor é,

Como , o valor necessário, devemos fazer outra iteração com um valor de maior.

Resultados de iteração adicionais são apresentados abaixo seguindo o mesmo raciocínio dos passos anteriores.

Após a Iteração 4, é alcançada uma convergência com . Então, a temperatura máxima da placa é,

Para o caso de temperatura uniforme, o procedimento para estimativa do coeficiente médio de transferência de calor é o mesmo. Então,