Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 6.Problemas - Ex. 36
Uma comporta basculante, que controla a taxa de escoamento de um canal simplesmente levantando ou abaixando uma placa vertical, normalmente é usada em sistemas de irrigação. Uma força é exercida sobre a comporta devido à diferença entre as alturas da água e e as velocidades de escoamento e a jusante e a montante da comporta, respectivamente. Desprezando as forças de cisalhamento da parede nas superfícies do canal, deduza relações para , e para a força que age em uma comporta basculante com largura durante um escoamento em regime permanente e uniforme.
Passo 1
O enunciado quer que a gente deduza três fórmula. Uma para a velocidade de escoamento do líquido que ainda não ultrapassou a comporta , outra para a velocidade de escoamento do líquido que já ultrapassou a comporta e, por fim, para a força que é exercida pelo líquido sobre a comporta. A imagem abaixo ilustra o significado dessas variáveis e mostra o volume de controle que escolhemos para deduzir as três equações.
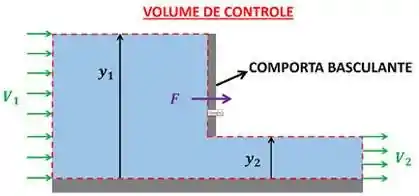
Conforme podemos ver pela figura, o volume de controle engloba o líquido.
Esse escoamento pode ser considerado escoamento em regime permanente, desprezando o acúmulo de energia e massa dentro do volume de controle. Além disso, como se trata do escoamento de um líquido, podemos considerar que o escoamento é incompressível. Logo:
onde é a densidade do líquido.
Por fim, a questão pede para desprezarmos as forças cisalhantes (forças viscosas). Isso quer dizer que os efeitos do atrito são desprezíveis. Em outras palavras, podemos usar a equação ode Bernoulli nesse escoamento! Nos dois passos aprenderemos a deduzir e .
Passo 2
Para encontrar expressões para as duas velocidades e , temos que aplicar a equação de conservação de massa e a equação de Bernoulli ao volume de controle. A equação de conservação de massa de um escoamento incompressível diz que a vazão volumétrica de entrada é igual à vazão volumétrica de saída .
onde é a área pela qual o líquido passa para entrar no volume de controle e é a área pela qual o líquido passa para sair do volume de controle. Essas duas áreas são iguais a altura multiplicada pela largura da comporta. Por causa disso:
Passo 3
Aplicando Bernoulli a uma linha de corrente do volume de controle, temos:
Como os pontos na altira e os pontos na altura estão em contato com a atmosfera (são superfícies livres), as duas têm pressão igual à pressão atmosférica. Isso quer dizer que a pressão manométrica do ponto a uma altua e a pressão manométrica do ponto a uma altua são iguas a:
Com esses novos dados, encontramos que:
Substituindo a outra fórmula de nessa equação:
Com essa informação podemos deduzir uma fórmula para .
Passo 4
Para encontrar uma expressão para a força , temos que usar a segunda lei de Newton (equação da quantidade de movimento) para escoamentos em regime permanente. Segue abaixo a equação da segunda lei para o volume de controle.
onde é o somatório de todas as forças que atuam no eixo , é a vazão mássica do líquido que passa pelo volume de controle e é o fator de correção do escoamento. O fator de correção para escoamentos com forças de cisalhamento desprezíveis vale . Logo:
Passo 5
Para saber quanto vale , temos que saber quais as forças que atuam horizontalmente no volume de controle. é uma dessas forças. O escoamento entrando no volume de controle exerce uma força sobre o volume de controle por causa da sua pressão média . Além disso, o escoamento saindo do volume de controle exerce uma força sobre o volume de controle por causa da sua pressão média . A figura abaixo mostra as forças.
Por isso, vale:
As pressões médias e são obtidas através das equações abaixo vindas da hidrostática.
Com essas novas informações, conseguimos achar uma fórmula para .
Passo 6
Igualando as duas expressões de , achamos uma fórmula para .