Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 6.Problemas - Ex. 31
Os bombeiros seguram um bocal na ponta de uma mangueira enquanto tentam apagar um incêndio. Se o diâmetro de saída do bocal é de e a taxa de escoamento da água é de , determine (a) a velocidade média de saída da água e (b) a força de resistência horizontal necessária para que os bombeiros segurem o bocal.
Passo 1
O enunciado pede que a gente calcule primeiro a velocidade média da água que sai do bocal. Para calcular isso, vamos precisar usar a fórmula de vazão volumétrica . A vazão volumétrica é igual à velocidade média da água multiplicada pela área pela qual a água passa para sair do bocal. Como o enunciado nos informou , podemos calcular através desse dado.
Mas falta saber calcular para acharmos . Como o enunciado diz que o diâmetro da área do bocal vale , podemos supor que a área pela qual a água sai é circular. Por isso, a fórmula de é:
Substituindo isso na equação da velocidade, achamos:
Passo 2
Antes de substituir os dados na fórmula de para achar essa velocidade média, precisamos converter a vazão volumétrica de para , dividindo ela por .
Além disso, precisamos converter o diâmetro de para , dividindo ela por .
Passo 3
Depois de calcular a velocidade média , o enunciado quer que a gente calcule a força horizontal que os bombeiros precisam fazer para manter o bocal parado. O primeiro passo para achar esse valor é escolhendo um volume de controle. Como queremos informações sobre o bocal, escolhemos um volume de controle que engloba o bocal e parte da mangueira.
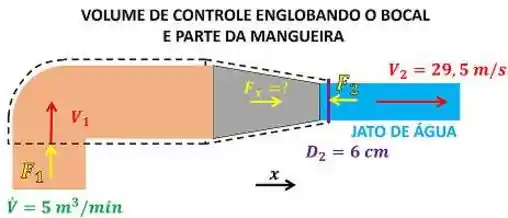
é a velocidade do jato de líquido entrando no volume de controle. Supomos que essa velocidade é vertical, considerando que a mangueira dobra em . Isso vai facilitar as contas. Esse escoamento de líquido saindo do bocal exerce uma força sobre o volume de controle por conta da pressão manométrica do jato de água. No entanto, como a água sai do bocal para a atmosfera, sua pressão é igual à pressão atmosférica. Ou seja, a pressão manométrica vale zero.
Isso quer dizer que a força vale zero também, porque é a multiplicação entre e .
O líquido entrando verticalmente pela mangueira exerce uma força vertical sobre o volume de controle.
No próximo passo vamos descobrir como calcular .
Passo 4
Agora que escolhemos o volume de controle, podemos usar a segunda lei de Newton nesse volume de controle. Para simplificar, o escoamento do volume de controle é considerado como sendo um escoamento em regime permanente. Como estamos interessados apenas nas forças horizontais (ao longo do eixo ), usaremos apenas a equação de quantidade de movimento (segunda lei de Newton) relativa ao eixo apenas.
Além disso, o volume de controle possui apenas uma corrente de fluido entrando horizontalmente e uma corrente saindo horizontalmente. Por causa de todos esses fatores, podemos usar a equação .
onde é o somatório das forças horizontais (no eixo ) sobre o volume de controle, é a vazão mássica do jato entrando e saindo do volume de controle. é o fator de correção para o escoamento que entra no volume de controle. é o fator de correção para o escoamento que sai do volume de controle. é a velocidade do jato no eixo que entra no volume de controle. é a velocidade do jato no eixo que sai do volume de controle.
Esta é a equação de quantidade de movimento no eixo (segunda lei de Newton) para um escoamento em regime permanente, com uma corrente entrando e outra saindo. No próximo passo descobriremos quanto vale cada termo dessa fórmula.
Passo 5
As forças horizontais exercidas sobre o volume de controle são e . Só que vale zero. Por isso, a força resultante é igual a .
Se nós considerarmos que o escoamento é incompressível (com densidade constante), podemos calcular pela equação abaixo.
A densidade da água na temperatura ambiente e a pressão atmosférica pode ser considerada igual a:
Como a velocidade é vertical, sua componente horizontal vale:
O fator de correção para o escoamento de água saindo do volume de controle vale , porque esse escoamento é um jato.
Substituindo todos esses dados na segunda lei de Newton, achamos:
Passo 6
Substituindo os dados na equação de , achamos seu valor.