Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 123

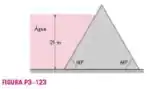
A água de um reservatório com 25   m de profundidade mantida no seu interior por uma parede com 150   m de largura cuja seção transversal é um triângulo equilátero, como mostra a Figura P3-123. Determine (a) a forca total (hidrostática + atmosférica) que age sobre a superfície interna da parede e sua linha de ação e (b) a intensidade da componente horizontal dessa fora. Considere P a t m = 100   k P a .

Passo 1

Bom galera, nesse problema temos água em um reservatório sendo contida por uma parede triangular. O que devemos fazer é determinar a força total e a componente horizontal.

Para isso, vamos considerar que a pressão atmosférica atua nos lados do reservatório e, portanto, podemos ignorá-la.

Passo 2

Começamos dividindo de forma a termos um triangulo retângulo, com hipotenusa e catetos. Assim, podemos calcular o comprimento da superfície da parede pelo seno:

sin ⁡ 60 ° = 25 b         ∴       b = 28,9   m

Para acharmos a força resultante, precisamos calcular a pressão média na superfície que é multiplicada pela área da placa

F R = P m é d A

Essa pressão média é a pressão absoluta! Logo,

F R = ( P a t m + ρ g h c ) A

Daí é só substituirmos os dados, lembrando que a área do triângulo é base vezes altura, temos:

F R = 100   k P a + 1000 k g m 3 × 9,81 m s 2 × 25   m 150   m × 28,9 m 1 N 1 k g m s 2

F R = 10,63 × 10 8 N

Passo 3

Para o calculo da componente horizontal da força hidrostática é simplesmente:

F H = F R sin ⁡ θ

Logo,

F H = 10,63 × 10 8 N sin ⁡ 60 ° = 9,21 × 10 8 N

Prontinho!!

Resposta

(a) F R = 10,63 × 10 8 N

(b) F H = 9,21 × 10 8 N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A cúpula hemisférica na Figura P2.91 pesa 30 kN e está cheia de água e presa ao piso por seis parafusos igualmente espaçados. Qual é a força exigida em cada parafuso para manter a cúpula fixa ao chão?
Um tanque de água com diâmetro de 4 m consiste em dois meios-cilindros, cada um pesando 4,5 kN/m, aparafusados juntos como mostra a Figura P2.92. Se o apoio das tampas nas extremidades for desprezado,
Água sob pressão enche o tanque da Figura P2.100. Calcule a força hidrostática líquida na superfície cônica ABC.
Na Figura P2.93, uma carcaça esférica de um quadrante de raio R está submersa em líquido de peso específico gama e profundidade hR. Encontre uma expressão analítica para a força hidrostática resultant
A caixa fechada em camadas da Figura P2.101 tem seções transversais quadradas horizontais em toda a sua altura. Todos os fluidos estão a 20°C. Calcule a pressão manométrica do ar se (a) a força hidros