Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 55

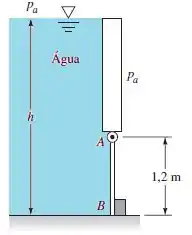
A comporta AB na figura abaixo tem 1,5 m de largura, está articulada em A e limitada por um limitador em B. A água está a 20°C. Calcule (a) a força no limitador B e (b) as reações em A se a profundidade de água é h = 2,85 m.

Passo 1

O primeiro passo é calcular o centroide de AB. Bem, se tratando de uma placa na vertical, o centroide de AB nada mais é do que o meio desse cara, show?

A gente sabe que a profundidade de água é 2,85m, então a profundidade que o centroide está é em h C G = 2,85 + 0,6 - 1,2 = 2,25   m .

Passo 2

(a) A força hidrostática total que atua na comporta será dada por:

F = ρ á g u a g h C G A c o m p o r t a = 979 x 10 x 2,25 x 1,2 x 1,5 = 39649   N

Precisamos calcular agora YCP

y C P = - I X X s e n θ h C G A   = - b L 3 12 s e n θ h C G A = - 1,5 x 1,2 3 12 s e n 90 ° 2,25 1,5   x   1,2 = - 0,054   m

Fazendo agora um balanço de momento na nossa comporta, sabendo que ela está em equilíbrio temos:

∑ M A = B X 1,2 - 39649 0,654 = 0

B X = 22685,93   N

Passo 3

(b) As forças de reação em A são dadas pelo equilíbrio de forças:

∑ F x = 0 = 39649   N - 22685,93 - F A x → F A x = 17 k N

∑ F z = 0 = F A z + P e s o c o m p o r t a → F A z = P e s o c o m p o r t a

Resposta

  1. B X = 22685,93 N
  2. F A x = 17   k N   e   F A Z = P e s o c o m p o r t a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar o mínimo valor de z para o qual a comporta da figura girará em torno de ponto O , se a comporta é retangular e tem largura 2m .
A comporta da figura, em forma de 1 4 de cilindro, tem peso desprezível. Determinar a relação γ 1 / γ 2 entre os pesos específicos dos líquidos, para que a comporta não gire em torno do ponto O . Dado
A comporta A B C D E F da figura, articulada no extremo A , mantém-se na condição de equilíbrio pela ação da força H aplicada em F . Sendo γ = 10000N / m 3 e a largura da comporta igual a 1m , determi
O reservatório da figura possui uma parede móvel A B , articulada em A . Sua largura é 1,5m e está em equilíbrio nas condições indicadas. Calcular:A força que age na face direita da comporta devido à
Um tanque com 5m de comprimento e 4m de altura contém água a uma profundidade de 2,5m quando não está em movimento e é aberto para a atmosfera através de uma ventilação no meio. Agora o tanque é acele