Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 52

O exemplo 2.5 calculou a força na placa AB e sua linha de ação, usando a abordagem de momento de inércia. Alguns professores dizem que é mais instrutivo calcular esses valores por integração direta das forças de pressão. Usando a figura abaixo, (a) encontre uma expressão para a variação de pressão p ( ξ ) ao longo da placa, (b) integre essa expressão para encontrar a força total F.

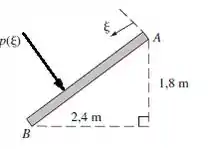
Passo 1

Bem, vamos lá!! O cálculo de pressão num ponto, de acordo com a hidrostática, pode ser dado por:

P = ρ g h

Agora, vamos escrever a forma diferencial total dessa equação, afinal, a gente agora não quer avaliar só em ponto, mas sim ao longo de toda a placa, beleza?

d P = ρ g d h

Passo 2

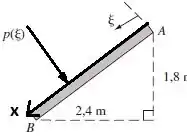
Note que podemos considerar um triângulo no desenho onde de posse do valor de θ , podemos dizer que s e n θ = h x → h = x   s e n θ

Para descobrirmos quem é o ângulo que precisamos, basta lembrarmos que:

tan ⁡ θ = C O C A = 1,8 2,4 = 0,75 → θ = 37 °

d P = ρ g d ( x s e n θ )

d P = d F d A → d F = d P d A = ρ g d x   s e n θ d A

F = ρ g s e n θ ∬ x   d x d z

Sabe-se que dZ varia de 0 até Z e dx de 0 até L, onde Z e L são largura e comprimento da placa.

F = ρ g s e n θ z L 2 2

Resposta

a   P = ρ g d ( x s e n θ )

b   F = ρ g s e n θ z L 2 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um sistema está equipado com dois medidores de pressão e um manômetro, como mostra a figura P 3 - 115 . Para Δ h = 8c m , determina a diferença de pressão Δ P = P 2 - P 1 .
Repita o Problema 3-110 levando em conta a expansão térmica d água â medida que ela é aquecida de 20 ° C até a temperatura de ebulição 100 ° C .
A variação da pressão com a densidade em uma camada de gás espessa é dada por P = C ρ n , onde C e n são constantes. Observando que a variação de pressão em uma camada de fluido diferencial com espess
Um bule de chá com infusor na parte superior é usado para fazer chá, como mostra a Figura P 3 - 110 . O infusor pode impedir parcialmente que o vapor escape, fazendo com que a pressão no bule suba e o
Considere um tubo em U preenchido com mercúrio, exceto por 18c m de altura na parte superior, como mostra a Figura P 3 - 109 . O diâmetro do braço direito do tubo em U é D = 2c m e o diâmetro do braço