Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 67

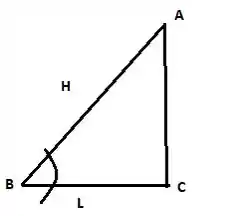
Generalizando o problema P2.66 da seguinte maneira: represente a distancia AB por H, a distância BC por L e o ângulo ABC por θ . Considere que o material da barragem tenha densidade d. A largura da barragem seja b. Considere ainda que não haja percolação de água por baixo da barragem. Encontre uma relação analítica entre a densidade d e o ângulo crítico θ c para a qual a barragem tombará à direita. Use a sua relação para calcular θ c para o caso especial de d = 2,4 (concreto).

Passo 1

Vamos lembrar em primeiro lugar que para uma placa, a sua linha de atuação é 2/3 do seu comprimento. Pela geometria a gente também tem que L = H c o s θ e que a altura da barragem é dada por H s e n ( θ ) .

A força que atua na superfície AB é dada por F = ρ g h C G A = ρ g H 2 s e n θ ( H b )

E como visto, sua linha de atuação é em 2/3 do comprimento de uma placa, ou seja 2 H 3

Passo 2

A distância da força que atua em C pode ser dado por 2 H 3 - L c o s θ . Por sua vez, a força peso é dada por W = g ρ V = ρ g L 2 H b s e n θ em uma distância equivalente a L/3.

Passo 3

A soma dos momentos no ponto C será dada por:

∑ M C = 0 = ρ g - H 2 s e n θ H b H 3 - L c o s θ - d ρ g L 2 H s e n θ b L 3

Resolvendo, temos que:

cos 2 ⁡ θ c = 1 3 + d

Resposta

cos 2 ⁡ θ C = 1 3 + d

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a placa inclinada AB com comprimento L na figura abaixo. (a) A força hidrostática sobre a placa é igual ao peso da água que está faltando acima da placa? Se não for, corrija essa hipótese. D
Em 1960, o batiscafo Trieste de Auguste e Jacques Picard bateu um recorde descendo a uma profundidade de 10912 m no Oceano Pacífico, próximo de Guam. A esfera que alojava o passageiro tinha 2,1 m de d
A comporta AB tem comprimento L e largura b, está articulada em B e tem peso desprezível. O nível h do líquido permanece no topo da comporta para qualquer ângulo θ . Encontre uma expressão analítica p
A comporta B da figura abaixo tem 30 cm de altura, 60 cm de largura e é articulada no seu topo. Qual a profundidade h de água na qual terá início a abertura da comporta?
A comporta AB na figura abaixo é uma massa homogênea de 180 kg, 1,2 m de largura, é articulada em A e está apoiada sobre um fundo liso em B. Todos os fluidos estão a 20°C. Para qual profundidade h da