Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 72
Um tanque de sedimentação para abastecimento municipal de água tem 2,5 m de profundidade, e a água a 20°C escoa continuamente a 35 cm/s. Calcule o comprimento mínimo do tanque para garantir que todo o sedimento (d = 2,55) caia até o fundo, considerando diâmetros de partículas maiores que (a) 1 mm e (b) 100 .
Passo 1
E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)! Primeiro passo é DESENHAR!!!
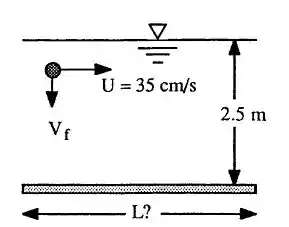
(a) Vamos lá, essa questão é mais trabalhosa do que difícil!!!! Então bora que bora!!
Primeira coisa que vou fazer é pedir pra você pegar as propriedades da água
O enunciado nos diz que as partículas viajam a 35 cm/s, mas elas precisam cair numa determinada velocidade, certo?
Passo 2
As partículas viajam na velocidade da corrente de fluido que está passando (sem arrasto na horizontal) e cai na velocidade com arrasto igual ao peso líquido da lindona da partícula na água, que é dada por:
Onde sabemos que que pode ser visto na figura 7.16b do livro. Sabemos também que onde h = 2,5 m.
Passo 3
(a) Para
Vamos começar aqui nosso processo de iteração, chutando e ver no gráfico da figura 7.16 que temos um Reynold em torno de 140, se liga!
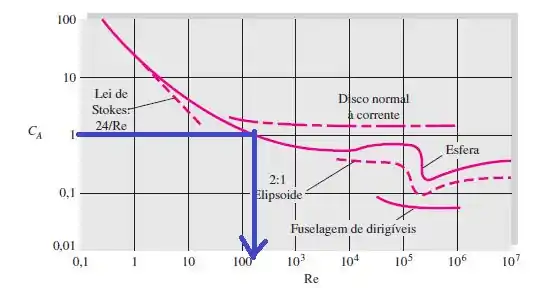
Aí com esse valor de calculamos o valor de . Você agora com esse valor, recalcularia Reynold e leria na figura acima qual é o novo valor de . Se bater próximo de 1 que foi o valor que você chutou inicialmente, já temos um processo convergido.
No caso, o processo convergiu com o chute de .
Com isso conseguimos calcular o valor de
Passo 4
(a) Para
Vamos começar aqui nosso processo de iteração, chutando e ver no gráfico da figura 7.16 igual fizemos no passo anterior. Cara, observa que agora sua partícula é menor ainda, isso quer dizer que provavelmente o Reynold dessa parada abaixou já muito mais, então eu iria começaria a leitura na curva de lei de Stokes, o que daria pra gente um Re = 0,75 mais ou menos!
Note que esse resultado faz muito sentido, uma vez que a partícula é menor, ela vai demorar mais para sedimentar e por isso precisamos ter um comprimento maior.