Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 68
A comporta AB em forma de triangulo isósceles da figura abaixo está articulada em A e pesa 1500N. Qual é a força horizontal P necessária no ponto B para que haja equilíbrio?
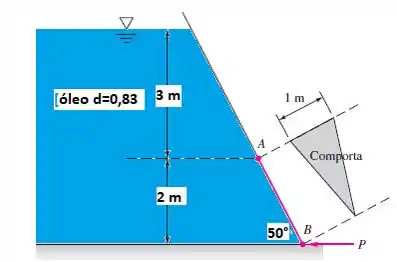
Passo 1
Vamos desenhar um diagrama de corpo livre pra começarmos a entender o problema.
Bem, a gente sabe que pra força de pressão, ela sempre estará perpendicular a uma superfície, certo? Então pra ela, qualquer superfície sempre estará na horizontal! Então vamos calcular qual é essa distância entra A e B.
Foi visto também que para um triângulo, seu centroide estará a 1/3 da distância entre seu lado AB!! Isso diz que
Vamos agora calcular a força F (setinha azul), que seria a força hidrostática realizada na superfície da comporta, beleza?
Mas qual será essa área da estrutura triangular??
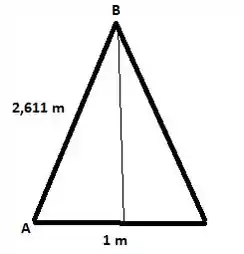
Por Pitágoras, tiramos que:
Onde h é a altura desse triângulo e concluímos que , portanto a área desse triângulo será:
Passo 2
Para calcularmos força, vamos precisar do balanço de forças de momento e pra isso vamos antes precisar encontrar qual é a linha de atuação da força hidrostática, beleza?
Passo 3
Vamos agora colocar as novas cotas pra enxergarmos melhor as coisas!!
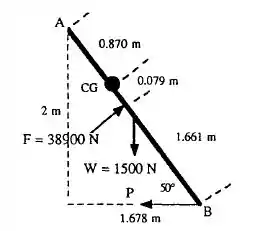
Vamos fazer o somatório dos momentos em torno de A, e, como estamos em equilíbrio, essa soma deve ser zero!!
A distância que da força aplicada em B até o ponto A é dado por 2m, logo L1 = 2
A distância da força hidrostática será dada pela soma do centroide (1/3 x 2,611) com a altura da linha de atuação calculada, YCP, ou seja, temos
Por sua vez, a força peso está atuando no centroide da comporta, ou seja, em (2,611/2) = 0,559 m.