Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 52

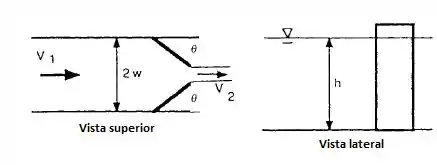
A comporta vertical de um canal d’água está parcialmente aberta, como abaixo. Considerando que o nível de água não varia e que a distribuição de pressões é hidrostática, deduza uma expressão para a força na direção do escoamento, Fx, sobre uma das metades da comporta em função de ( ρ ,   h ,   w ,   θ ,   V 1 ) . Aplique seu resultado no caso de água a 20°C, V 1 = 0,8   m / s , h = 2 m , w = 1,5   m e θ = 50 ° .

Passo 1

Bem, se você olhar bem, temos que a vazão deve ser igual na entrada e na saída para que se respeita a conservação de massa considerando um fluido incompressível.

V 1 W h = V 2 B h → V 2 = V 1 W B = V 1 1 1 - s e n θ

Passo 2

Vamos aplicar nosso volume de controle em torno do nosso sistema como abaixo!

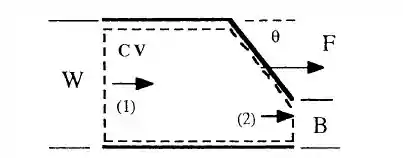
Considerando que B = W - W s e n θ . Vamos ter que fazer uma abstração adoidada aqui, que é dizer que a profundidade de água será constante, fazendo assim temos que a força de pressão hidrostática líquida no nosso sistema será zero, fazendo com que o nosso balanço de forças se reduza a:

∑ F X = F c o m p o r t a ,   f l u i d o = m ˙ V 2 - m ˙ V 1 = m ˙ V 2 - V 1 = ρ W h V 1 V 2 - V 1

Vimos no passo 2 quem é nosso V 2 , certo?

F c o m p o r t a ,   f l u i d o = ρ W h V 1 V 2 - V 1 = ρ W h V 1 2 1 1 - s e n θ - 1

Então a força que o fluido exercerá na comporta deve ser igual em módulo a força encontrada acima, porém, com sinal oposto, certo?

F f l u i d o , c o m p o r t a = - ρ W h V 1 2 1 1 - s e n θ - 1

Passo 3

Para o nosso caso em particular, considerando as dimensões dadas pelo enunciado, temos que:

W = 1,5 m

θ = 50 °

B = W 1 - s e n θ = 0,351   m

V 1 = 0,8   m / s

V 2 = V 1 1 - s e n θ = 3,42 m s

ρ = 998 k g m 3

h = 2

F f l u i d o , c o m p o r t a = | - ρ W h V 1 2 1 1 - s e n θ - 1 |

F f l u i d o , c o m p o r t a = 998 2 1,5 0,8 2 1 1 - s e n 50 - 1 = 6300   N

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No antigo Egito, vasos circulares cheios de água eram por vezes utilizados como relógios primitivos. Os vasos tinham um formato tal que, à medida que a água drenava pelo fundo, o nível da superfície d
Um fluido incompressível de viscosidade desprezível é bombeado com uma vazão volumétrica total Q por uma superfície porosa para o interior de uma pequena fresta entre placas paralelas estreitamente es
Uma corrente de fluido incompressível movendo-se a baixa velocidade sai de um bocal apontado diretamente para baixo. Considere que a velocidade em qualquer seção reta seja uniforme e despreze efeitos
Um líquido incompressível de viscosidade desprezível é bombeado com uma vazão volumétrica total Q através de dois pequenos orifícios para dentro de uma pequena fresta entre discos paralelos estreitame
Projete uma clepsidra (relógio de água Egípcio) – um recipiente do qual água é drenada por gravidade através de um orifício no fundo e que indica o tempo pelo nível da água remanescente. Especifique a