Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 17

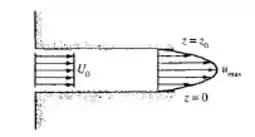
O escoamento permanente incompressível entre placas paralelas tem velocidade uniforme na entrada u = U o = 8   c m / s , desenvolvendo-se a jusante num perfil laminar parabólico, u = a z z o - z , em que a é uma constante. Se z o = 4   c m e o fluido é óleo SEA 30, a 20°C, qual será o valor de u m á x em cm/s?

Passo 1

Aqui vai ser bem tranquilo, galera! Então te convido a lançar um lindo “lerigou” e vamos que vamos!

Primeira coisa é lembrar que pra um escoamento incompressível: tudo o que entra tem que ser igual a tudo que tá saindo.

Q e = Q s a i

Passo 2

Como temos um valor de velocidade constante na entrada, então podemos dizer que a vazão será dada pelo produto da velocidade com a área transversal de escoamento. Na saída, a gente já vai ter um perfil, então vamos precisar integrar nosso perfil na área de escoamento, certo? Vamos dizer que a largura das placas tem comprimento b.

Q e = U 0 b z 0

Q s a i = ∫ 0 z 0 ∫ 0 b a z z 0 - z d z d y = a b z 0 3 6

Igualando as vazões, temos:

U 0 b z 0 = a b z 0 3 6 → a = 6 U 0 z 0 2

Passo 3

Bem, para um perfil laminar, temos que a velocidade máxima será sempre dada no centro de um tubo ou no centro da distância entre as placas.

Então, se a gente pega o perfil de velocidade, substitui a e faz com que z = z 0 2 , teremos o valor da nossa velocidade máxima.

u = a z z o - z → u m á x = a z 0 2 z 0 - z 0 2 = a z 0 2 4

Vamos substituir a e TCHARAAAAMMMMM, vamos ter nosso valor de velocidade máxima!!!

u m á x = 6 U 0 z 0 2 z 0 2 4 = 3 2 U 0 = 3 2 8 = 12   c m / s

Resposta

u m á x = 12   c m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A massa de gás no interior de um botijão varia segundo a lei: m t = m 0 - β t , onde β = c t e . Sendo ρ s a massa específica do gás na seção de saída, calcular a velocidade média nessa seção, cuja ár
A figura mostra uma seringa para injeções, com as respectivas dimensões. Se a velocidade do êmbolo é 0,25 cm/s e a velocidade do líquido na agulha é 25 cm/s, qual a porcentagem de líquido desperdiçada
No tubo em U da figura, de seção de área A, oscila, em torna da posição de equilíbrio, uma coluna de comprimento total L de um líquido admitido ideal. Determinar o período T da oscilação.
Um reservatório cilíndrico de exploração de água possui um diâmetro interno igual a 3 m, e uma altura de 3 m. Existe somente uma entrada com diâmetro igual a 10 cm, uma saída com diâmetro de 8 cm, e u
Com o passar do tempo, o ar escapa dos pneus de alta pressão de uma bicicleta por migração através dos poros da borracha. É regra corrente dizer que um pneu perde pressão a uma taxa de “ 6,9k P ap o r