Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 126
Projete uma clepsidra (relógio de água Egípcio) – um recipiente do qual água é drenada por gravidade através de um orifício no fundo e que indica o tempo pelo nível da água remanescente. Especifique as dimensões do recipiente e o tamanho do orifício de drenagem; indique a quantidade de água necessária para encher o recipiente e o intervalo de tempo ao fim do qual ele deve ser novamente enchido. Trace um gráfico do raio do vaso em função da elevação.
Passo 1
Tá legal! Vamos começar esse exercício ilustrando o relógio egípcio e desenhando nosso volume de controle:
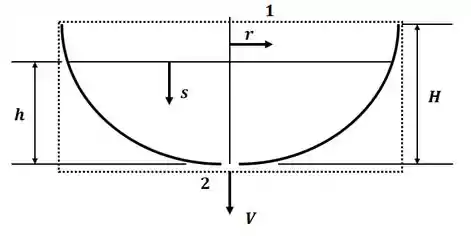
Vamos começar esse exercício aplicando o princípio da continuidade para o sistema, nesse caso, teremos:
Então, nesse caso, teremos ar entrando na superfície 1 e água saindo na superfície 2, então a equação se torna:
Só que, como nós sabemos que e que , podemos simplificar os termos referentes ao ar na equação acima, pois eles serão desprezíveis perto daqueles da água, então, a equação se torna:
Sabemos que a variação de volume do reservatório é dado em função da velocidade de descida , que por sua vez, é dada por:
E a variação de volume é dada por:
Então, substituindo o valor de , temos:
Agora vamos substituir o valor da expressão para na equação da continuidade, então, temos:
Passo 2
Agora vamos aplicar a equação de Bernoulli entre a superfície superior do reservatório e o orifício de saída, então, temos:
Tá legal, como ambos os pontos 1 e 2 estão expostos ao ambiente, temos e os termos de pressão se cancelam. Sabemos também que e que . Considerando o nível , então, temos , dessa forma, a equação de Bernoulli se torna:
Então, agora, vamos substituir a expressão encontrada para na expressão para encontrada no passo 1, então, temos:
Passo 3
Agora para encontrar uma expressão para o volume de água necessário para que o relógio funcione por horas, vamos começar encontrando o nível para horas de operação, que será dado pela velocidade vezes o tempo , então, temos:
Dessa forma, o volume total será:
Substituindo a expressão para no limite de integração e a expressão encontrada para no passo 1, temos:
Substituindo a expressão encontrada no passo 2 para a velocide de saída, temos:
Resolvendo a integral, temos:
Substituindo os limites de integração, obtemos a relação desejada para o volume:
Passo 4
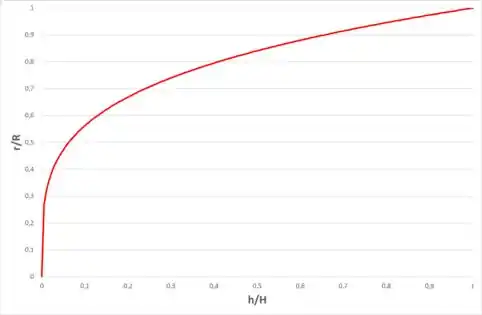
Agora vamos plotar o gráfico do raio da vaso em função da elevação, que foi a equação obtida no passo 2, dada por:
Como não temos o valor das constantes, vamos parametrizar por e , então, temos:
