A concentração da luz solar sobre células fotovoltaicas é desejável, pois os espelhos e lentes concentradores são menos caros do que o material fotovoltaico. Considere a célula solar fotovoltaica do Exemplo 3.3. Uma célula fotovoltaica de é irradiada com energia solar concentrada. Como as lentes concentradoras são feitas em vidro, elas absorvem da irradiação no lugar da superfície superior da célula solar, como no Exemplo 3.3. A irradiação restante é refletida para fora do sistema ou é absorvida no material semicondutor de silício da célula . A célula é resfriada por ar direcionado paralelamente às suas superfícies superior e inferior. A temperatura e a velocidade do ar são e , respectivamente, e a superfície inferior é coberta com uma tinta de alta emissividade, .
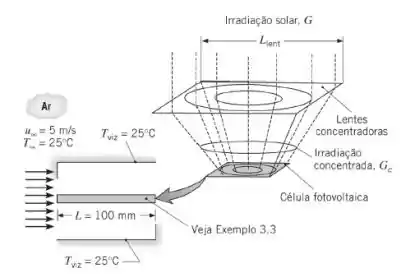
(a) Determine a potência elétrica produzida pela célula fotovoltaica e a temperatura do silício, em um sistema que tem uma lente concentradora quadrada com , que concentra a irradiação nela incidente para uma área menor ocupada pela célula fotovoltaica. Suponha que a temperatura da lente concentradora seja de e que ela não interfira no desenvolvimento da camada-limite sobre a superfície superior da célula. As camadas-limite nas superfícies superior e inferior são levadas a condição de turbulentas na aresta frontal do material fotovoltaico.
Passo 1
Bora resolver essa questão?
Se liga e vamos lá!
Começamos o nosso problema obtendo algumas propriedades a respeito dos materiais do nosso sistema:
:
:
:
:
Pela Tabela A.4, para o ar a :
Agora, devemos desenhar o circuito térmico do nosso sistema:
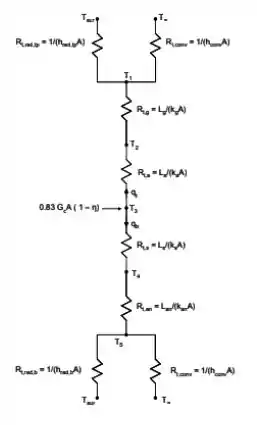
Passo 2
Calculando as resistências térmicas:
Passo 3
Analisando as camadas limite superior e inferior desarmadas.
Calculando :
Calculando :
Calculando :
Calculando :
Passo 4
Do circuito termal:
Onde:
E
Do mesmo modo:
E
A eficiência da conversão solar em elétrica é:
Resolvendo as equações:
Assim, temos que a potência elétrica produzida pela célula fotovoltaica é:
E assim terminamos a nossa questão, até a próxima!