Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 117

Na concepção de um receptor central para coleta de energia solar, um grande número de heliostatos (refletores) fornece um fluxo solar concentrado de qs= 80.000 W/m2 a um receptor, que se encontra posicionado no topo de uma torre.

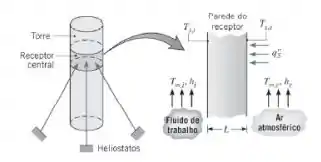
A parede do receptor recebe um fluxo solar sobre sua superfície externa, que está exposta ao ar atmosférico, com T∞,e = 300 K e he = 25 W/(m2 · K). A superfície externa é opaca e difusa, com uma absortividade espectral de αλ = 0,9 para λ > 3 μm e αλ = 0,2 para λ > 3 μm. A superfície interna está em contato com um fluido de trabalho (um líquido pressurizado) com T∞,i = 700 K e hi = 1000 W/(m2 · K). A superfície externa também está exposta a uma vizinhança a Tviz = 300 K. Se a parede é fabricada com um material resistente a altas temperaturas com k = 15 W/(m · K), qual é a espessura mínima L necessária para assegurar que a temperatura da superfície externa não exceda Ts,e = 1000 K? Qual é a eficiência de coleta associada a essa espessura?

Passo 1

Fala aí! Partiu fazer essa questãozinha!

Vamos começar anotando nossos dados:

T ∞ ,   e = 300   K h e = 25   W / m ² . K T ∞ ,   i = 700   K h i = 1000   W / m ² . K

k = 15   W / m . K α 1 = 0,9 λ < 3   μ m α 2 = 0,3   λ > 3   μ m

q s " = 80000   W / m ² T s u r = 300   K

Precisamos achar a espessura mínima, nas condições pedidas, e a eficiência… então vamos para as continhas!

Passo 2

Para calcular a espessura mínima, vamos começar fazendo um balanço de energia:

E e n t = E s a i

α S   .   q S " + α s u r   .   G s u r = ε   .   σ   .   T s ,   e 4 + h e   .   T s ,   e - T ∞ ,   e + T s ,   e - T ∞ ,   i L k + 1 h i

α S   .   q S " + α s u r   .   σ   .   T s u r 4 = ε   .   σ   .   T s ,   e 4 + h e   .   T s ,   e - T ∞ ,   e + T s ,   e - T ∞ ,   i L k + 1 h i

Precisamos encontrar esse α S :

α S = α 1   .   F 0 → 3   μ m + α 2   .   F 3 → ∞

Para achar F 0 → 3   μ m , vamos fazer:

λ   .   T = 3   .   5800 = 17400   μ m   .   K

Indo na tabela 12.2, temos que:

F 0 → 3   μ m = 0,979 F 3 → ∞ = 1 - F 0 → 3   μ m = 0,021

Ele será então:

α S = 0,9   .   0,979 + 0,2   .   0,021

α S = 0,885

E para encontrar nossa emissividade vamos ter:

ε S = ε 1   .   F 0 → 3   μ m + ε 2   .   F 3 → ∞

Temos que achar o F 0 → 3   μ m novamente, porque agora a temperatura é diferente, vamos fazer:

λ   .   T = 3   .   1000 = 3000   μ m   .   K

Indo na tabela 12.2, temos:

F 0 → 3   μ m = 0,273 F 3 → ∞ = 1 - F 0 → 3   μ m = 0,727

Ficaremos com:

ε S = 0,9   .   0,273 + 0,2   .   0,727

ε S = 0,391

E sendo α s u r = 0,2 , podemos ir ao que interessa!

Passo 3

Agora sim podemos encontrar a espessura:

0,885   .   80000 + 0,2   .   5,67   .   10 - 8   .   300 4 = 0,391   .   5,67   .   10 - 8   .   1000 4 + 25   .   1000 - 300 + 1000 - 700 L 15 + 1 1000

L = 0,129   m

Primeira parte ok! Falta a eficiência, vamos nessa!

η = q u s e " q s "

η = T s ,   e - T ∞ ,   i L k + 1 h i q s "

η = 1000 - 700 0,129 15 + 1 1000 80000

η = 0,391

ou

η = 39,1 %

Prontinho! Arrasamos!

Resposta

L = 0,129   m η = 39,1 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cilindro, com 30m m de diâmetro e 150m m de comprimento, é aquecido em um grande forno cujas paredes se encontram a 1000K , enquanto ar a 400K e a uma velocidade de 3m / s circula no seu interior.
Um pequeno bloco de alumínio anodizado, a 35 ° C , é aquecido em um grande forno cujas paredes são difusas e cinzas com ε = 0,85 e mantidas a uma temperatura uniforme de 175 ° C . O revestimento anodi
Um gato de rua gosta de dormir sobre o telhado de nosso barracão no fundo do quintal. A superfície do telhado é de uma folha metálica galvanizada gasta pelo tempo ( ε=0,65eα S=0,8 ) . Considere um dia
A superfície exposta de um amplificador de potência de um receptor utilizado em um satélite terrestre, com área de 130m m por 130m m , tem um revestimento opaco, cinza e difuso, com uma emissividade d
Um disco metálico circular, com diâmetro de 0,4m , é firmemente posicionado contra o solo em uma região estéril, horizontal, onde a terra está a uma temperatura de 280K . A temperatura do céu efetiva