Uma fina lâmina de vidro é utilizada no telhado de uma estufa e é irradiada conforme ilustrado.

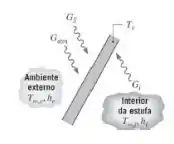
A irradiação compreende o fluxo solar total GS, o fluxo Gatm devido à emissão atmosférica (radiação do céu) e o fluxo Gi devido à emissão das superfícies internas. Os fluxos Gatm e Gi estão concentrados na região IV distante (λ 8 μm). O vidro também pode trocar energia por convecção com as atmosferas no exterior e no interior da estufa. O vidro pode ser considerado totalmente transparente para λ

1. Admitindo condições de regime estacionário, com todos os fluxos radiantes uniformemente distribuídos ao longo das superfícies e o vidro caracterizado por uma temperatura uniforme Tv, escreva um balanço de energia apropriado para uma área unitária do vidro.
2. Para Tv = 27°C, hi = 10 W/(m2 · K), GS = 1100 W/m2 , T∞,e = 24°C, he = 55 W/(m2 · K), Gatm = 250 W/m2 e Gi = 440 W/m2 , calcule a temperatura do ar ambiente no interior da estufa, T∞,i.

Na letra b, vamos calcular a temperatura, usando a equação que separamos na letra a, show?

Vamos primeiro achar os termos que faltam:

Vamos encontrar o :

Para achar o , vamos calcular:

E visitando a tabela 12.2, teremos:

Vamos ficar então com:

Nossa temperatura será:

Prontinho! Mandamos muito bem!