Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 79
Ar no interior de uma câmara a é aquecido por convecção, com , por uma parede com de espessura, condutividade térmica de e com geração uniforme de calor a uma taxa de . Para evitar que qualquer calor gerado no interior da parede seja perdido para o lado de fora da câmara, a e , uma fita aquecedora elétrica muito fina é colocada sobre a superfície externa da parede para fornecer um fluxo térmico uniforme, .
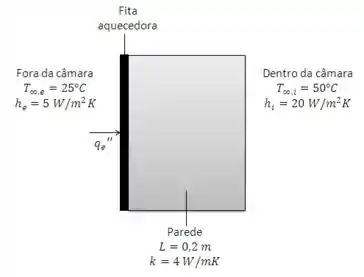
(a) Esboce a distribuição de temperaturas na parede, em um sistema de coordenadas , para a condição na qual nenhum calor gerado no seu interior é perdido para o lado de fora da câmara.
(b) Quais são as temperaturas nas superfícies da parede, e , para as condições da parte (a)?
(c) Determine o valor de que deve ser fornecido pela fita aquecedora de modo que todo o calor gerado no interior da parede seja transferido para o interior da câmara.
(d) Se a geração de calor na parede for interrompida enquanto o fluxo fornecido pela fita aquecedora permanecer constante, qual será a temperatura em regime estacionário, , na superfície externa da parede?
Passo 1
O item (a) nos pede para começar esboçando o perfil de temperatura no interior da parede. Vamos supor que a transferência de calor ocorre em regime permanente e apenas na direção . Na parede a transferência de calor ocorre apenas pelo mecanismo de condução:
Integrando dos dois lados:
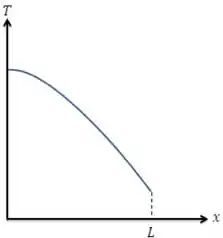
Então, o perfil de temperatura será parabólico. Além disso, sabemos que não há transferência de calor para fora da fita, então
Portanto, o perfil de temperatura na parede é parabólico, com gradiente de temperatura igual a zero na posição :
Passo 2
Para o item (b) devemos encontrar as temperaturas e . Para isso, vamos definir as constantes e . Do item (a):
Para :
Então o perfil de temperaturas é:
Vamos agora aplicar um balanço de energia na parede :
Em regime permanente e considerando que não há produção de energia ():
Da equação do perfil:
Vamos agora para o item (c). Neste item devemos encontrar o fluxo para que não haja fluxo de calor da parede para o ambiente externo. Para isso, vamos fazer o balanço de energia na parede .
Em regime permanente e considerando que não há produção de energia ():
Passo 3
Agora no item (d) devemos encontrar a nova temperatura de equilíbrio para a condição em que a parede deixa de produzir energia. Para isso, vamos fazer um balanço de energia considerando que o regime estacionário já foi atingido:
Desta vez temos apenas a fita eletromagnética fornecendo energia ao sistema e, perda de calor pelas duas paredes. Então:
Para definir as taxas de perda de calor em cada parede vamos calcular as resistências envolvidas em cada caso. Começando pela parede , teremos apenas transferência de calor por convecção. Então:
Para a parede temos condução na parede e convecção no ambiente interno:
E
E a resistência equivalente na parede é:
Voltando para o balanço iremos substituir
Ficamos então com:
Resposta
(a)
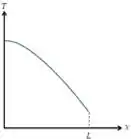
(b)
(c)
(d) .