Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 34
Condução unidimensional, em regime estacionário, com geração de energia interna uniforme ocorre em uma parede plana com espessura de e condutividade térmica constante igual a Nessas condições, a distribuição de temperaturas tem a forma. A superfície em x = 0 está a uma temperatura. Nessa superfície, há convecção com um fluido a com A superfície em é isolada termicamente.
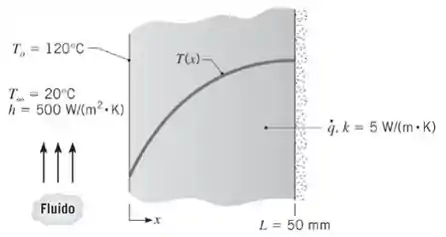
(a) Utilizando um balanço de energia global na parede, calcule a taxa volumétrica de geração de energia.
(b) Determine os coeficientes e aplicando as condições de contorno na distribuição de temperaturas especificada. Use os resultados para calcular e representar graficamente a distribuição de temperaturas.
(c) Considere condições nas quais o coeficiente de transferência de calor por convecção seja dividido por dois, com a taxa volumétrica de geração de energia permanecendo inalterada. Determine os novos valores de e e use os resultados para representar graficamente a distribuição de temperaturas. Sugestão: note que não é mais.
(d) Sob condições nas quais a geração volumétrica de energia é dobrada e o coeficiente por convecção permanece inalterado determine os novos valores de e e represente graficamente a distribuição de temperaturas correspondente. Referindo-se aos resultados das partes (b), (c) e (d) como Casos 1, 2 e 3, respectivamente, compare as distribuições de temperaturas para os três casos e discuta as influências de e nas distribuições.
Passo 1
Bora para mais uma questão? 😊 Aqui nós temos uma condução em estado estacionário com geração interna uniforme de energia em uma parede plana onde a distribuição de temperatura tem forma quadrática. A superfície em é dada e o limite em é isolado termicamente.
Aqui nós precisamos calcular a taxa interna de geração de energia, determinar os coeficientes e , plotar a distribuição de temperatura e rotular como Caso 1. Além disso, devemos determinar novos valores para e para condições em que o coeficiente de convecção é dividido pela metade e a taxa de geração permanece inalterada, traçar a distribuição de temperatura e rotular como Caso 2.
Por fim, devemos, determinar novos valores para e para condições em que a taxa de geração é dobrada e o coeficiente de convecção permanece inalterado, traçar a distribuição de temperatura e rotular como Caso 3. Então, vamos lá!
Passo 2
Começando pela letra (a), vamos utilizar um balanço de energia global na parede para calcular a taxa volumétrica de geração de energia.
Onde,
Então,
Isolando o ,
Substituindo os valores:
Passo 3
Na letra (b), queremos os coeficientes e aplicando as condições de contorno na distribuição de temperaturas . Os coeficientes podem ser especificados aplicando as condições de contorno em e .
A condição de contorno em, condição da superfície de convecção é:
Onde,
Então,
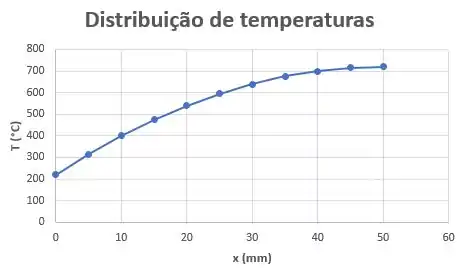
Substituindo os valores, temos:
Já a condição de contorno em, superfície adiabática ou isolada, é:
Onde,
Então,
Como a superfície em é conhecida, encontramos:
O gráfico desta alternativa é:
Passo 4
Na letra (c), queremos calcular novos valores de e de modo que o coeficiente de transferência de calor por convecção seja dividido por dois. Ou seja:
Onde e outros parâmetros permanecem inalterados, exceto que Para . Podemos determinar e para a expressão da distribuição de temperatura repetindo as análises das partes (a) e (b). Então, faremos um balanço de energia geral na parede:
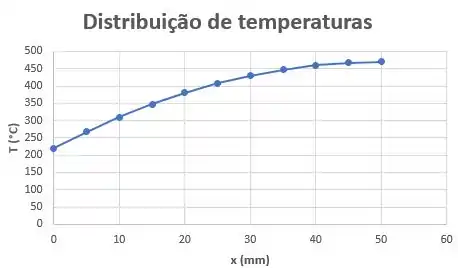
Para o balanço de energia na superfície em que , temos:
Já para o balanço de energia na superfície em que , temos:
Graficamente, temos:
Passo 5
Na letra (d), queremos calcular novos valores de e sob condições nas quais a geração volumétrica de energia é dobrada e o coeficiente por convecção permanece inalterado, ou seja:
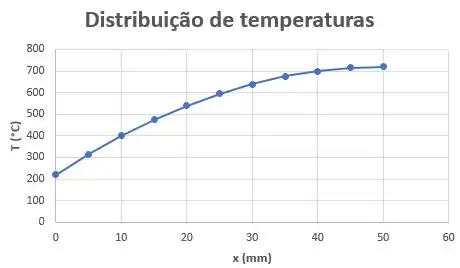
Onde os outros parâmetros permanecem inalterados, exceto para . Seguindo o raciocínio da alternativa (c), os coeficientes para a nova distribuição de temperatura são:
E o gráfico é:
Resposta
- , e
- , e
- , e
