Em uma parede plana com espessura e condutividade térmica há geração de calor volumétrica uniforme a uma taxa , enquanto transferência de calor por convecção ocorre em suas duas superfícies cada uma exposta a um fluido com temperatura. Em condições de regime estacionário, a distribuição de temperaturas no interior da parede tem a forma, sendo, e está em metros. A origem da coordenada encontra-se no plano central da parede.
(a) Esboce a distribuição de temperaturas e identifique características físicas significativas.
(b) Qual é a taxa volumétrica de geração de calor na parede?
(c) Determine os fluxos térmicos nas superfícies, e . Como esses fluxos estão relacionados com a taxa de geração de calor?
(d) Quais são os coeficientes de transferência de calor por convecção nas superfícies e?
(e) Obtenha uma expressão para a distribuição de fluxos térmicos, . O fluxo térmico é nulo em algum local? Explique algumas características significativas desta distribuição.
(f) Se a fonte da geração térmica for subitamente desativada qual é a taxa de variação da energia acumulada na parede neste instante?
(g) Com , qual temperatura a parede atingirá após um longo período de tempo? Que quantidade de energia tem que ser removida da parede pelo fluido, por unidade de área da parede para ela atingir esse estado? A massa específica e o calor específico do material da parede são e respectivamente.
Passo 1
Essa questão é grandinha mas com muita calma, carinho e paciência a gente consegue resolver ela juntos, ta bem?
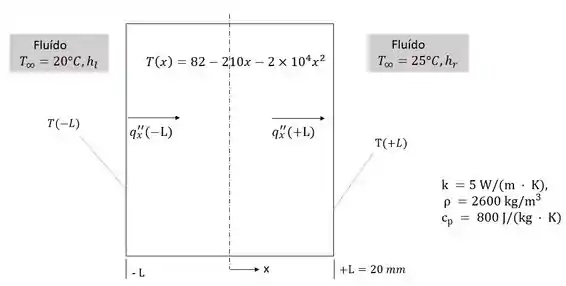
A questão nos pede para esboçar a distribuição de temperatura e identificar as características físicas significativas, determinar e os fluxos de calor da superfície e dizer como esses fluxos estão relacionados à taxa de geração. Além disso, precisamos calcular os coeficientes de convecção nas superfícies e obter uma expressão para a distribuição do fluxo de calor, explicando as características significativas da distribuição.
Se a fonte de geração de calor for subitamente desativada , precisamos dizer qual é a taxa de mudança de energia armazenada neste instante. Por fim, temos que determinar a temperatura que a parede atingirá eventualmente com e determinar a energia que deve ser removida pelo fluido por unidade de área da parede para atingir esse estado.
Ufa! Muito coisa, eu sei, mas vamos respirar fundo e seguir juntos! 😊
Passo 2
Para resolver essa questão vamos considerar que estamos em condição de estado estacionário, a taxa volumétrica de geração de calor é uniforme e as propriedades são constantes.
Na letra (a), queremos esboçar a distribuição de temperaturas, ou seja:
Lembrando as unidades dos coeficientes:
Podemos esboçar o gráfico:
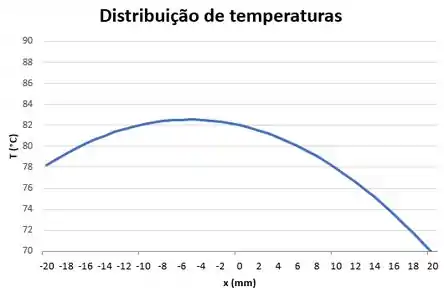
Aqui eu deixei a distância em para facilitar a visualização do gráfico, ta bem? E as características significativas são:
(1) Forma parabólica;
(2) O máximo não ocorre no plano médio, ;
(3) O gradiente na superfície é maior do que em.
Além disso, vamos encontrar também que e para usar depois na letra (d).
Passo 3
Na letra (b) queremos a taxa volumétrica de geração de calor na parede e, para isso, vamos substituir a expressão da distribuição de temperatura na equação de difusão de calor:
Onde,
Então,
Isolando o :
Passo 4
Na letra (c) queremos encontrar os fluxos térmicos nas superfícies, que podem ser determinados usando a lei de Fourier e a expressão da distribuição de temperatura.
Onde,
Então,
Analogamente,
A questão também nos pergunta como esses fluxos estão relacionados com a taxa de geração de calor. A partir de um balanço de energia geral na parede, temos:
Ou,
Passo 5
Na letra (e), queremos os coeficientes de transferência de calor por convecção nas superfícies. Eles podem ser determinados a partir dos fluxos de calor de convecção que são iguais aos fluxos de condução nos limites, e vamos utilizar os balanços de energia para chegar em:
Passo 6
Na letra (e), queremos uma expressão para a distribuição de fluxos térmicos, e saber se ele é nulo em algum local. Para isso vamos usar a lei de Fourier com a distribuição da temperatura.
Substituindo os valores, temos:
A distribuição é linear com a coordenada e a temperatura máxima ocorrerá no local em que ,
Passo 7
E na letra (f)? Aqui nós queremos a taxa de variação da energia acumulada na parede quando Neste caso, a equação de difusão de calor para a condução transiente é:
No instante em que isso ocorre, a distribuição de temperatura ainda é. O termo à direita representa a taxa de armazenamento de energia por unidade de volume,
Passo 8
Na (g), e última \o/, queremos saber, com , qual temperatura a parede atingirá após um longo período de tempo e que quantidade de energia tem que ser removida da parede pelo fluido, por unidade de área da paredepara ela atingir esse estado.
Sem geração de calor, a parede vai ficarem equilíbrio com o fluido,, em que Para determinar a energia que deve ser removida da parede para atingir esse estado, vamos aplicar a conservação de energia. O estado “inicial” é o correspondente à distribuição de temperatura no estado estacionário, , e o estado “final” tem. Usamos como condição de referência para os termos de energia.
Onde,
Resposta
(a)

(1) Forma parabólica;
(2) O máximo não ocorre no plano médio, ;
(3) O gradiente na superfície é maior do que em.
(b)
(c)
(d)
(e)
(f)
(g)