Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 53
O conduto do Problema 11.46 é ajustado com um novo revestimento de filme plástico (n = 0,010). Determine a nova profundidade de escoamento se a descarga permanece constante a 2,42 m³/s.
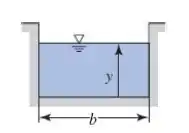
Passo 1
Beleza! Sabemos que a equação da descarga para o sistema é dada por:
Então precisamos escrever a equação da descarga em função da altura . Com o auxílio da tabela de geometria fornecida nessa seção, temos:
Passo 2
Substituindo o valor para a largura do canal dado no Problema 11.46, temos:
Passo 3
Então, substituindo os valores conhecidos na equação de descarga, temos:
Então, para resolver essa equação, precisamos da ajuda de uma calculadora, que nos dá:
Resposta
Exercícios de Livros Relacionados
Considere o canal em formato de V de ângulo arbitrário da Figura P10.41. Se a profundidade for y, (a) encontre uma expressão analítica para a velocidade de propagação c 0 de uma pequena onda de pertur
O escoamento uniforme da água em um canal largo de alvenaria com declividade de 0,02° ocorre sobre uma elevação de 10 cm como na Figura P10.59. Isso resulta em uma pequena depressão na superfície da á
Na Figura P10.62, considere V 0 = 6 m sey 0 = 1m . Se a altura máxima da elevação for de 35 cm, calcule (a) o número de Froude sobre o topo da elevação e (b) o aumento máximo no nível da superfície da
For the river fl ow of Prob. P10.48, fi nd the depth y2 that hasthe same specifi c energy as the given depth y1 5 12 ft.These are called conjugate depths. What is Fr2?
A wide, clean-earth river has a flow rate q 5 150 ft3/(s ? ft).What is the critical depth? If the actual depth is 12 ft, whatis the Froude number of the river? Compute the criticalslope by (a) Manning