Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 52

Determine a descarga na qual o canal do Problema 11.51 escoa repleto.

Passo 1

Beleza! Para podermos encontrar a descarga, dada pela equação:

Q = 1 n A R h 2 3 S b 1 2

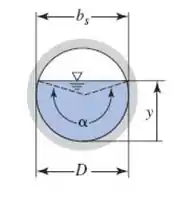
Precisamos encontrar todos esses parâmetros antes. Então, vamos começar com a geometria do canal, sabemos, do esquema da figura e como o enunciado disse que o canal escoa completo, então teremos:

α = 180 °

Passo 2

Agora, com os valores dados no enunciado e o valor de α , com o auxílio da tabela de geometria a seguir, conseguimos encontrar os termos que precisamos:

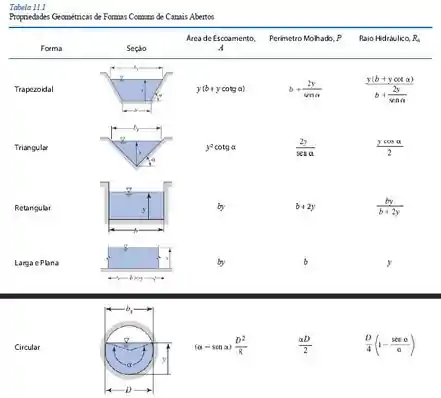
Então, para o nosso caso, teremos (lembrando de utilizar o ângulo em radianos):

A = α - s e n α D 2 8 = π - s e n π 1 2 8 → A = 0,393   m 2

R h = D 4 1 - s e n α α = 1 4 1 - s e n π 2,09 → R h = 0,25   m

Então, agora só falta obter o valor de n , para isso, vamos recorrer a tabela a seguir:

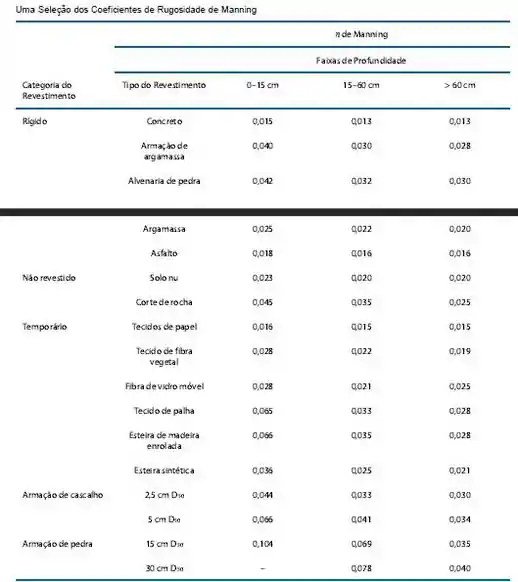
Beleza, não temos o valor do n para o aço corrugado, então, pesquisando na internet, obtemos um valor de:

n = 0,02

Passo 3

Então, a equação para a descarga será:

Q = 1 n A R h 2 3 S b 1 2 = 1 0,02 0,393 0,25 2 3 0,01 1 2 → Q = 0,780   m 3 / s

Resposta

Q = 0,780   m 3 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o canal condutor Venturi mostrado. O fundo é horizontal e o escoamento pode ser considerado sem atrito. A profundidade a montante é 0,3m e a profundidade a jusante é 0,22m . A largura a mont
Em uma seção de um canal retangular com 3m de largura, a profundidade é 0,09m para uma descarga de 0,57m 3 / s . Um ressalto suave com 0,03m de altura é colocado sobre o fundo do canal. Determine a va
Um canal retangular horizontal com 0,9m de largura contém uma comporta. A montante da comporta a profundidade é de 1,8m ; a profundidade a jusante é de 0,27m . Estime a vazão volumétrica no canal.
A figura mostra o escoamento através de uma comporta. Estime a profundidade da água e a velocidade depois da comporta (bem antes do ressalto hidráulico).
Find the critical depth of the brick channel in Prob. P10.34for both the 4- and 8-ft widths. Are the normal flows subcritical or supercritical?