Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas - Ex. 59
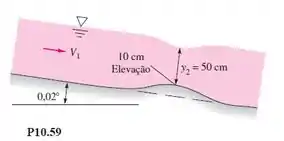
O escoamento uniforme da água em um canal largo de alvenaria com declividade de 0,02° ocorre sobre uma elevação de 10 cm como na Figura P10.59. Isso resulta em uma pequena depressão na superfície da água. Se a profundidade mínima da água sobre a elevação for de 50 cm, calcule (a) a velocidade sobre a elevação e (b) a vazão por metro de largura.
Passo 1
Lets go, família! Bora resolver mais uma.
Para uma estrutura de alvenaria, temos . Uma vez que o nível de água diminui com a elevação, o fluxo ascendente é subcrítico. Sabendo disso, teremos que:
Temos e .
Nosso escoamento pode ser dado por:
Vamos resolver as duas equações simultaneamente, com isso, encontraremos, para ,
Daí,
Lembrando que para um escoamento subcrítico temos .
Resposta
Exercícios de Livros Relacionados
O canal do Problema 11.49 possui uma inclinação no fundo igual a 0,00193. Determine a profundidade normal para a descarga dada após a instalação de um novo revestimento de plástico (n = 0,010).
O conduto do Problema 11.46 é ajustado com um novo revestimento de filme plástico (n = 0,010). Determine a nova profundidade de escoamento se a descarga permanece constante a 2,42 m³/s.
Uma cuba semicircular de aço corrugado, com diâmetro D = 1m , carrega água a uma profundidade y = 0,25m . A inclinação é de 0,01. Determine a descarga.
Determine a descarga na qual o canal do Problema 11.51 escoa repleto.
A descarga através do canal do Problema 11.49 é aumentada para 10 m³/s. Determine a profundidade normal correspondente, se a inclinação do fundo for 0,00193.