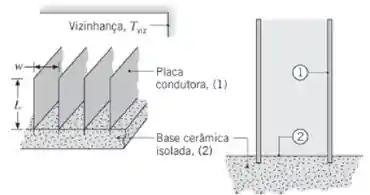
Condutores elétricos, na forma de placas paralelas com comprimento L = 40 mm, têm uma aresta fixada a uma base cerâmica isolada termicamente e são espaçados entre si por uma distância . As placas estão expostas a uma grande vizinhança isotérmica a . As superfícies do condutor (1) e da cerâmica (2) são difusas e cinzas, com emissividades e , respectivamente. Para uma dada corrente de operação nos condutores, sua temperatura é .

1. Determine a potência elétrica dissipada em uma placa condutora por unidade de comprimento (normal à página), considerando apenas a troca de calor por radiação. Qual é a temperatura da base isolada, ?
2. Determine e quando há transferência de calor por convecção nas superfícies com uma corrente de ar a 300 K, com um coeficiente de transferência de calor .

Olhando a figura abaixo para achar o fatore de forma entre (2) e (3):

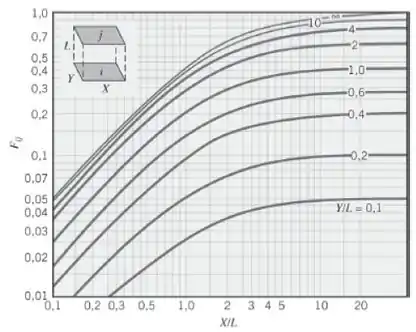
Sabendo que:

E neste caso:

Então:

Olhando no gráfico:

Aplicando a soma para a superfície 3:

Pela reciprocidade:

Por simetria:

Então agora é só substituir:

Reorganizando:

Mas ainda precisamos da temperatura em 2, certo? Assumindo que:

Para achar vamos usar a relação que já sabemos:

Substituindo as potências:

Neste caso:

Substituindo:

Nós ainda não temos , certo? Mas existe uma relação que podemos usar, a equação 13.31:

Substituindo tudo:

Agora basta achar a temperatura:

Na letra (b) queremos achar a quando há transferência de calor por convecção nas superfícies com uma corrente de ar a 300 K, com um coeficiente de transferência de calor , ok?

Então neste caso, o calor que entra por radiação irá ser transferido por convecção e radiação:

Substituindo:

Como nós não temos nem vamos precisar lembrar que:

Substituindo o que sabemos:

Agora, como a superfície 2 é isolada:

Como temos três variáveis vamos precisar de três equações, então podemos usar:

Substituindo:

Resolvendo as três equações simultaneamente:

Colocando tudo isso no calor que entra:

E é isso aí galerinha, bora seguir ??