Revestimentos aplicados a longas tiras metálicas são curados pela instalação das tiras ao longo das paredes de um longo forno com seção transversal quadrada.

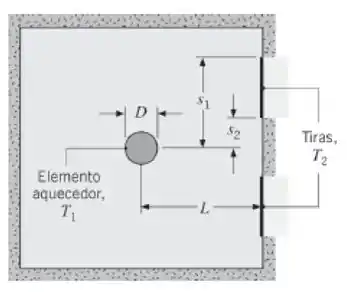
As condições térmicas no interior do forno são mantidas por um longo bastão de carbeto de silício (elemento aquecedor), que tem diâmetro D = 20 mm e opera a T1 = 1700 K. Cada uma das duas tiras sobre uma parede lateral tem a mesma orientação em relação ao bastão (s1 = 60 mm, s2 = 20 mm, L = 80 mm) e opera a T2 = 600 K. Todas as superfícies são difusas e cinzas com ε1 = 0,9 e ε2 = 0,4. Admitindo que o forno esteja isolado termicamente em todas as suas superfícies à exceção das superfícies das tiras e desprezando os efeitos convectivos, determine a demanda de energia por unidade de comprimento (W/m).

é a área do elemento aquecedor (área de um cilindro) , dividida pelo seu comprimento:

é a área das tiras, divididas pelo comprimento, lembrando que temos duas tiras:

Precisamos achar e , pela regra da soma:

Pela regra da reciprocidade:

Temos um cilindro (elemento aquecedor) paralelo com um retângulo (tira), então, podemos usar a relação da tabela do livro pra achar :

Tiramos do enunciado:

Não precisa se preocupar com as unidades, porque elas vão se cancelar:

Então podemos achar :

Com isso achamos :

Para achar :

Calculando:

Lembrando que e os dados do enunciado:

E juntando todas as informações que descobrimos no Passo 2:

Substituindo:

Calculando, achamos:

Uhuuuul!!!