Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 13.Problemas - Ex. 15
Determine o fator de forma entre as superfícies retangulares mostradas na Fig. P13–15.
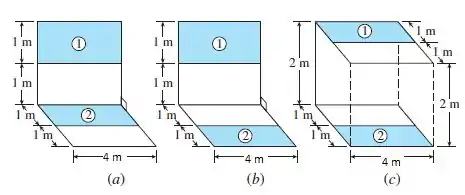
Passo 1
Boora pra mais uma galerinha??
Vamos começar com a figura (a) !
Uma relação muito importante que poderemos usar aqui é:
Quando acharmos nós poderemos usar a relação da reciprocidade e achar o que queremos, .
Como as superfícies 2 e 3 estão perpendiculares entre si nós poderemos usar o gráfico abaixo:
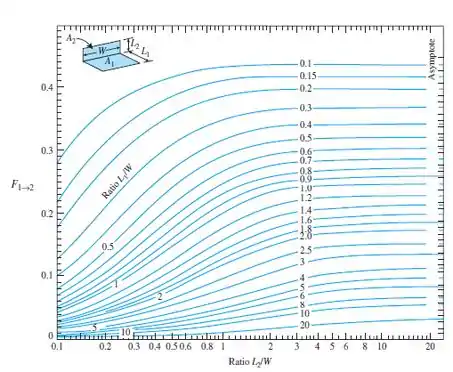
Então nós precisamos da razão para as superfícies 1 e 3, certo?
Se:
Então nossa razão será:
Quando nós olhamos no gráfico:
Como a superfície 2 também está perpendicular à superfície 1 e 3, vamos achar a razão para a superfície 13, ok?
Quando olhamos no gráfico:
Agora nós podemos lançar estes dados na primeira equação que vimos:
Passo 2
Olha só!! Já demos um passo muito grande!!
Mas ainda não achamos o que precisávamos, e para isso usaremos a relação da reciprocidade:
Como a largura e o comprimento de todas as superfícies são iguais:
Sendo assim:
Para a letra (a) tá pronto, mas ainda precisamos das demais !!
Passo 3
Na figura (b) temos as estruturas 2 e 4 perpendiculares às superfícies 1 e 3:
Achando as razões:
Olhando no gráfico:
E a próxima:
Se e :
Substituindo na igualdade que temos:
E o que fazemos com isso?
Usamos a regra da reciprocidade e vocês verão que vamos chegar lá:
Sabendo das áreas:
Então:
Isso ainda não resolve nosso problema, mas se vocês lembrarem desta relação a coisa muda de figura:
O termo é igual ao da figura (a), não é?
Sendo assim:
Com isso nós finalizamos a letra (b), vamos continuar?
Passo 4
Só precisamos da letra (c), não é?
Vamos começar analisando a superfície 24 em paralelo à superfície 13:
Usando o gráfico abaixo:
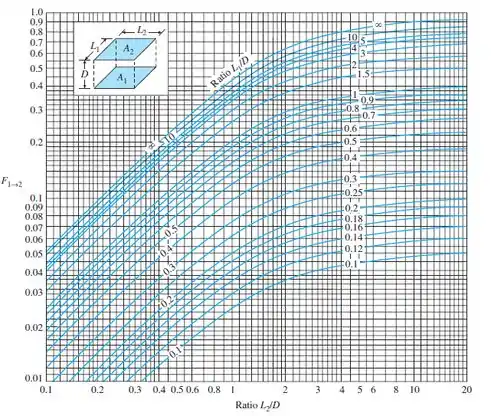
Quando nós olhamos no gráfico:
Com o somatório nós temos que:
Usando a regra de simetria:
Então:
Substituindo:
Passo 5
Ainda não achamos nada, mas para ficar um passo mais perto do que precisamos nós vamos usar a regra da reciprocidade:
Isolando:
Calculando a área:
E substituindo:
Usamos a mesma relação que nos passos anteriores:
Para finalizar nós precisamos achar o termo como são retângulos paralelos faremos a mesma coisa que fizemos no Passo 4:
Usando o gráfico:
Substituindo:
E fiiim !!