Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 46
Considere o aquecedor de água descrito no Problema 1.48. Desejamos, agora, determinar a energia necessária para compensar as perdas de calor que ocorrem enquanto a água está armazenada na temperatura especificada de 55°C. O tanque de armazenamento cilíndrico (com extremidades planas) possui uma capacidade de 100 galões e espuma de uretano é usada para isolar todas as suas superfícies (lateral e extremidades) do ambiente, que apresenta uma temperatura média anual de 20°C. A resistência à transferência de calor é dominada pela condução no isolante e pela convecção natural no ar, com h ≈ 2 W/(m2 · K). Se aquecimento por meio de uma resistência elétrica é usado para compensar as perdas e o custo da energia elétrica é de $0,08/(kW · h), especifique as dimensões do tanque e do isolante para um custo anual associado às perdas de calor inferior a $50.
Passo 1
Beleza galerinha, vamos lá! Para minimizar a perda de calor, devem ser selecionadas as dimensões do tanque que minimizem a área total de superfície, As,t.
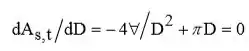
Que nos dá:
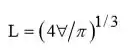
Passo 2
Por um custo anual de perda de calor de $50 e um custo unitário de energia elétrica de $0,18/kWh
A taxa de perda de energia é, portanto
A perda total de calor através das paredes laterais e das extremidades é
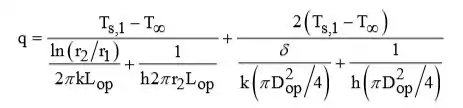
Passo 3
Resolvendo esse monstro:
