Em uma partícula esférica de raio há geração térmica uniforme a uma taxa . A partícula é encapsulada por uma casca esférica com raio externo , que é resfriada pelo ar ambiente. As condutividades térmicas da partícula e da casca são e , respectivamente, sendo = .
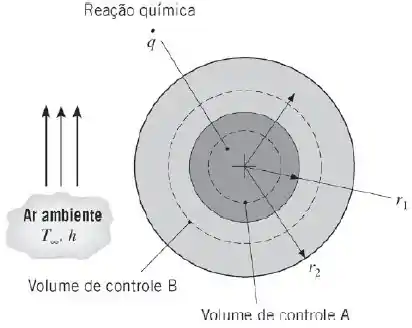
(a) Aplicando o princípio da conservação de energia no volume de controle esférico , que é posicionado em uma posição arbitrária no interior da esfera, determine uma relação entre o gradiente de temperatura, , e o raio local, , para .
(b) Aplicando o princípio da conservação de energia no volume de controle esférico , que é posicionado em uma posição arbitrária no interior da casca esférica, determine uma relação entre o gradiente de temperatura, , e o raio local, , para .
(c) Em coordenadas , esboce a distribuição de temperaturas em .
Passo 1
Vamos lá! primeiro vamos entender nosso problema, o problema diz que se trata de um sistema unidimensional com geração de energia, logo a troca de calor só ocorre em uma direção que no caso apresentado é a radial, vamos fazer nosso diagrama pra facilitar nossa vida.
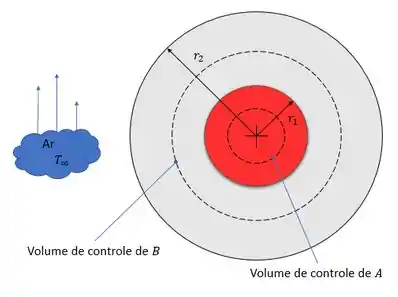
Origem e sentido do aquecimento da parede com geração de calor.
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
(a)
Tendo tudo isso em mente vamos a nossa letra (a) quer uma relação
Como nossa condução é unidimensional e há geração de energia, temos:
Sendo nossa energia gerada dada por:
Como nosso sistema não é isolado
Substituindo os resultados encontrados na equação do balanço de energia temos.
Isolando encontramos:
Passo 3
(b) Vamos seguir a mesma lógica do item entretanto nosso na parte
, assim temos:
Sendo nossa energia gerada dada por:
Como nosso sistema não é isolado
Substituindo os resultados encontrados na equação do balanço de energia temos.
Isolando encontramos:
Passo 4
(c) Vamos lá pra resolver isso precisamos integrar os resultados da letra (a) e da letra (b)
Primeiro para
Como a condição de contorno é.
Agora para
Como a condição de contorno é.
Simplificando:
Agora traçando nosso gráfico em função de temos:
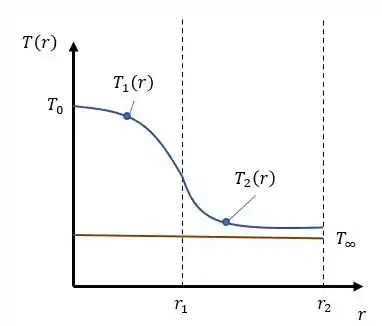
Obs: A primeira parte do gráfico se comporta em função de , logo é uma parábola com concavidade pra baixo, já a segunda parte segue como uma função de .
Isso é tudo pessoal! \o/

Resposta
Ei, a resposta está no passo a passo :)