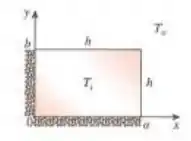
Considere uma extensa barra retangular de comprimento a no eixo x e largura b no eixo y que inicialmente está a uma temperatura uniforme T i . As superfícies da barra em x = 0 e y = 0 estão isoladas, enquanto há perda de calor nas outras duas superfícies por convecção para o meio ao redor a uma temperatura T ∞ com coeficiente de transferência de calor h . Assumindo que a condutividade térmica é constante, a transferência de calor é bidimensional transiente e não há geração de calor, expresse a formulação matemática (equação diferencial e condições inicial e de contorno) desse problema de condução de calor. Não resolva o problema.

A equação diferencial que rege o nosso problema é: ∂ 2 T ∂ x 2 + ∂ 2 T ∂ y 2 = 1 α ∂ T ∂ t Já as condições de contorno e inicial são: ∂ T ∂ x x = 0 = 0 ∂ T ∂ y y = 0 = 0 - k ∂ T ∂ x x = a = h T a , y , t - T ∞ - k ∂ T ∂ y y = b = h T x , b , t - T ∞ T x , y , 0 = T i

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 126

Considere uma extensa barra retangular de comprimento a no eixo e largura no eixo que inicialmente está a uma temperatura uniforme . As superfícies da barra em e estão isoladas, enquanto há perda de calor nas outras duas superfícies por convecção para o meio ao redor a uma temperatura com coeficiente de transferência de calor . Assumindo que a condutividade térmica é constante, a transferência de calor é bidimensional transiente e não há geração de calor, expresse a formulação matemática (equação diferencial e condições inicial e de contorno) desse problema de condução de calor. Não resolva o problema.

Passo 1

Um problema de calor bidimensional sempre é complicado de resolver. Contudo, ainda bem, só precisamos fazer a sua formulação matemática!

Para fazermos a formulação, é fundamental entendermos as condições que o nosso problema está sujeito. Desta forma, temos um problema de calor bidimensional em regime transiente, sem geração de calor e com condutividade térmica constante.

Como estamos trabalhando com um sólido retangular, utilizaremos o sistema de coordenadas retangular. Portanto, a equação diferencial que rege o nosso problema é:

Percebam que esta EDP é bem semelhante ao caso unidimensional. A única diferença é a adição de mais um termo, referente a segunda coordenada do problema!

Passo 2

Agora, vamos escrever as condições de contorno e inicial do nosso problema. Começaremos pelas superfícies isolantes. Por causa desta condição, não há condução de calor nestas paredes. Sendo assim, temos:

Agora, vamos analisar nas outras duas superfícies, as quais estão em contato com um fluido. Consequentemente, há convecção nestas duas superfícies. Portanto, temos as seguintes condições de contorno:

Por fim, temos a condição relativa ao tempo. Como a barra está inicialmente a uma temperatura , a nossa condição é:

Desta forma, temos as 5 condições de contorno do nosso problema!

Resposta

A equação diferencial que rege o nosso problema é:

Já as condições de contorno e inicial são:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

69 – Em uma instalação de processamento de alimentos, um contêiner esférico de raio interno r 1 = 40c m , raio externo r 2 = 41c m e condutividade térmica k = 1,5 W m ⋅ K é usado para armazenar água q

Repita o Prob. 2-89 para um fio de manganês ( k = 7,8 W // m * ° C ) .

Calor é gerado uniformemente a uma taxa de 10 (kW/m) de comprimento do fio de 0,2 cm de diâmetro de resistência elétrica de aço niquelado ( k = 10 W / m ⋅ ° C ) . Determine a diferença de temperatura

Considere uma grande placa de aço inoxidável de 3 cm de espessura ( k = 15,1W / m ⋅ K ) onde calor é gerado uniformemente a uma taxa de 5 ⋅ 10 5W / m 3 . Ambos os lados da placa estão expostos ao ambi

Em um reator nuclear, o combustível tem a forma de barras cilíndricas de urânio com 1 cm de diâmetro que são resfriadas externamente por água. Calor é gerado uniformemente nas barras ( k = 29,5W / m ⋅